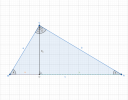
Áhá! Azóta is le akarom ellenőrizni, de még nem vettem rá magam. Viszont úgy tűnik, hogy most itt az ideje! A sok-sok összefüggést mind-mind az ábrám alapján írtam fel, amin be van jelölve minden. Én törekedtem arra, hogy mindent csakis a két adott értékkel számoljak ki, hogy pontosabbak legyenek az eredmények, de ez nem kötelező. Az eddig kiszámolt adatokkal is dolgozhatsz, amiket rögtön behelyettesíthetsz és megkapod az eredményt.

a) `a = "16 cm", b = "35 cm"`
Pitagorasz-tétel:
`a^2+b^2 = c^2 => c = sqrt(16^2+35^2) = sqrt 1481 ~~ "38,484 cm"`
`"tg"\ alpha = a/b => alpha = "tg"^"-1"(16/35) ~~ "24,567°"`
`beta = 90°-alpha ~~ "65,433°"`
Befogótétel:
`a^2 = x*c => x = 16^2/sqrt 1481 ~~ "6,652 cm"`
`b^2 = y*c => y = 35^2/sqrt 1481 ~~ "31,832 cm"`
Magasságtétel:
`m_c = sqrt(xy) = sqrt((16^2*35^2)/1481) = (16*35)/sqrt 1481 ~~ "14,552 cm"`

b) `a = "24 cm", c = "38 cm"`
`b = sqrt(38^2-24^2) = 2 sqrt 217 ~~ "29,462 cm"`
`sin alpha = a/c => alpha = sin^"-1"(24/38) ~~ "39,167°"`
`beta = 90°-alpha ~~ "50,833°"`
`x = a^2/c = 24^2/38 = 288/19 ~~ "15,158 cm"`
`y = b^2/c = (2 sqrt 217)^2/38 = 434/19 ~~ "22,842 cm"`
`m_c = sqrt(xy) = sqrt(288/19*434/19) = (24 sqrt 217)/19 ~~ "18,607 cm"`

c) `a = "6 cm", alpha = 52°`
`"tg"\ alpha = a/b => b = a/("tg"\ alpha) ~~ "4,688 cm"`
`sin alpha = a/c => c = a/sin alpha ~~ "7,614 cm"`
`beta = 90°-alpha = 38°`
`sin alpha = x/a => x = a sin alpha ~~ "4,728 cm"`
`cos alpha = y/b => y = b cos alpha = (a cos alpha)/("tg"\ alpha) ~~ "2,886 cm"`
`cos alpha = m_c/a => m_c = a cos alpha ~~ "3,694 cm"`

d) `beta = 80°, x = "13 cm"`
`cos beta = x/a => a = x/cos beta ~~ "74,864 cm"`
`"tg"\ beta = b/a => b = a\ "tg"\ beta = (x\ "tg"\ beta)/cos beta ~~ "424,575 cm"`
`cos beta = a/c => c = a/cos beta = x/cos^2 beta ~~ "431,125 cm"`
`alpha = 90°-beta = 10°`
`sin beta = y/b => y = b sin beta = ((x\ "tg"\ beta)/cos beta) sin beta = x\ "tg"^2 beta ~~ "418,125 cm"`
`"tg"\ beta = m_c/x => m_c = x\ "tg"\ beta ~~ "73,727 cm"`

e) `beta = 48°, m_c = "9 cm"`
`sin beta = m_c/a => a = m_c/sin beta ~~ "12,111 cm"`
`cos beta = m_c/b => b = m_c/cos beta ~~ "13,450 cm"`
`sin beta = b/c => c = b/sin beta = m_c/(sin beta cos beta) ~~ "18,099 cm"`
`alpha = 90°-beta = 42°`
`"tg"\ beta = m_c/x => x = m_c/("tg"\ beta) ~~ "8,104 cm"`
`"tg"\ beta = y/m_c => y = m_c\ "tg"\ beta ~~ "9,996 cm"`

Ha bármi kérdésed volna nyugodtan szólj!