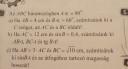Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Mértan
 Bodor Csilla
kérdése
Bodor Csilla
kérdése
369
C feladat megoldása kellene
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Általános iskola / Matematika
Válaszok
1 Epyxoid
{ Tanár }
megoldása
Epyxoid
{ Tanár }
megoldása
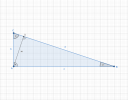
Mivel a két befogónak, `AB`-nek és `AC`-nek csak az arányuk van meg, vagyis az egymáshoz képesti viszonya, így ha közvetlenül írnánk fel a `B` csúcshoz tartozó szög szinuszát, ami a szemközti befogót és az átfogót hozza kapcsolatba, nem jutnánk semmire. Előtte még fel kéne írni még egy egyenletet a két befogóra - mivel már van egy -, mondjuk a Pitagoraszt, amivel két egyenletünk lesz a két ismeretlenre, vagyis meg tudjuk oldani!
`{(abs(AB)^2+abs(AC)^2 = abs(BC)^2), (abs(AB) = 3*abs(AC)):}`
`(3*abs(AC))^2+abs(AC)^2 = (sqrt 10)^2`
`9abs(AC)^2+abs(AC)^2 = 10`
`10abs(AC)^2 = 10 " /" :10`
`abs(AC)^2 = 1 " /" sqrt`
`abs(AC) = 1 " "` (negatív nem lehet, mivel egy alakzat oldaláról van szó)
Vagyis
`sin hat B = abs(AC)/abs(BC) = 1/sqrt 10 ~~ "0,316"`
Az átfogóhoz tartozó magasságot én a terület képletből vezetném le, ehhez viszont kéne a másik két oldal hossza is, úgyhogy ez a következő lépés... Ott hagytuk abba, hogy
`abs(AC) = "1 cm" => abs(AB) = 3*abs(AC) = 3*1 = "3 cm"`
A derékszögű háromszög területe egyenlő a befogók szorzatának felével, ugyanis a derékszögű háromszögnél az a különleges helyzet áll fenn, hogy a két befogó egymás magasságai is. Az egyik a másiknak és fordítva. Tehát:
`T = (abs(AB)*abs(AC))/2 = (3*1)/2 = 3/2 = "1,5 cm"^2`
Viszont a területet az átfogóval és a hozzátartozó - keresett - magassággal is felírhatjuk. Legyen ez a magasság `m`. Ekkor
`T = (abs(BC)*m)/2 => m = (2T)/abs(BC) = (2*3/2)/sqrt 10 = 3/sqrt 10 ~~ "0,949 cm"`
`{(abs(AB)^2+abs(AC)^2 = abs(BC)^2), (abs(AB) = 3*abs(AC)):}`
`(3*abs(AC))^2+abs(AC)^2 = (sqrt 10)^2`
`9abs(AC)^2+abs(AC)^2 = 10`
`10abs(AC)^2 = 10 " /" :10`
`abs(AC)^2 = 1 " /" sqrt`
`abs(AC) = 1 " "` (negatív nem lehet, mivel egy alakzat oldaláról van szó)
Vagyis
`sin hat B = abs(AC)/abs(BC) = 1/sqrt 10 ~~ "0,316"`
Az átfogóhoz tartozó magasságot én a terület képletből vezetném le, ehhez viszont kéne a másik két oldal hossza is, úgyhogy ez a következő lépés... Ott hagytuk abba, hogy
`abs(AC) = "1 cm" => abs(AB) = 3*abs(AC) = 3*1 = "3 cm"`
A derékszögű háromszög területe egyenlő a befogók szorzatának felével, ugyanis a derékszögű háromszögnél az a különleges helyzet áll fenn, hogy a két befogó egymás magasságai is. Az egyik a másiknak és fordítva. Tehát:
`T = (abs(AB)*abs(AC))/2 = (3*1)/2 = 3/2 = "1,5 cm"^2`
Viszont a területet az átfogóval és a hozzátartozó - keresett - magassággal is felírhatjuk. Legyen ez a magasság `m`. Ekkor
`T = (abs(BC)*m)/2 => m = (2T)/abs(BC) = (2*3/2)/sqrt 10 = 3/sqrt 10 ~~ "0,949 cm"`
Módosítva: 3 éve
0
- Még nem érkezett komment!