Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Trapez
 Bodor Csilla
kérdése
Bodor Csilla
kérdése
493
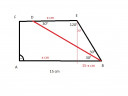
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Általános iskola / Matematika
Válaszok
2 kazah
válasza
kazah
válasza
Egy oldal és két szög ismeretében nem tudsz trapézt szerkeszteni, legfeljebb egy háromszöget. Jó lenne még egy szárhossz vagy valamilyen adat. Bár a szögekkel se sokra mész általános iskolás szinten.
1
-
segíítspls: Nem csodálom hogy neked nem megy

 3 éve
-3
3 éve
-3
-
kazah: Azt csodálnám, ha neked itt bármi menne, mert eddig még csak hangot hallottunk, ócsárolást és fikázást, de hasznos eredményt még nem. Bizonyíték, drágám, nem ígéret (mert az is volt már rendesen). Hajrá! 3 éve 0
-
Epyxoid: Valóban hiányzik még egy oldal... De ha te így is meg tudod oldani sp akkor hajrá! Most végre lemoshatsz minket a színről!
 3 éve
1
3 éve
1
-
segíítspls: Random D pontokat adsz meg. Húzd oda az F csúcshoz és tangensel ki tudod számolni az AF oldalt ami meggyezik a vele párhuzamos oldallal tangensel megint ki tudod számolni az x-et és ki volnod AB-ből x-et és tádám megvan az EF szakasz hossza. 3 éve 0
-
segíítspls: Segítsek tovább vagy eltudsz indulni? 3 éve -1
-
kazah: SEGÍÍTS!!!
 A teljes levezetést légyszives, ennyi segítségnyújtás után tartozol ennyivel.
3 éve
1
A teljes levezetést légyszives, ennyi segítségnyújtás után tartozol ennyivel.
3 éve
1
-
kazah: Elég lesz csak a rövid alapot kiszámolnod. 3 éve 0
-
segíítspls: Az előbb írtam le hogyan tudod kiszámolni az oldalakat hát nem figyelsz? 3 éve 0
-
segíítspls: Vagy nem ismered a szögfüggvényeket? 3 éve 0
-
kazah: figyelek, mennyi lett a rövid alap? 3 éve 1
-
segíítspls: 10 cm a rövid alap 3 éve 0
-
kazah: Tangenst meg még nem tanulnak általános iskolában. 3 éve 1
-
kazah: Ennyi, hogy benyögsz egy számot? Ez elég gyatra... 3 éve 0
-
segíítspls: Honnan veszed hogy általános iskolás? Csak abba a kategóriába van. 3 éve 0
-
segíítspls: Számold ki te is és meglátod hogy annyi. 3 éve 0
-
kazah: Ha abban a kategóriában van a feladat, akkor a megoldást is úgy kell kezelni. 3 éve 0
-
segíítspls: Ezért inkább oda írod hogy nem lehet megoldani xdddd sírok rajtad esküszöm 3 éve -1
-
kazah: Hát ez most sem sikerült neked, sajnálunk... majd legközelebb. 3 éve 0
-
Epyxoid: Jó gondolat sp, csak hogy sehol sincs megadva, hogy a `B` csúcsnál lévő szög szögfelezője az áthalad az `F` csúcson. Ha így lenne, akkor ez le volna írva, de nincs, így nem élhetünkezzel a kényelmes feltételezéssel. De ha így szólna a feladat, akkor valóban működne az, amit írsz. 3 éve 0
-
kazah: Cáfold meg, hogy nem lehet megoldani. Leírod ide a megoldás menetét és majd elbíráljuk.
 3 éve
1
3 éve
1
-
segíítspls: A feladat írja hogy BF átló hogy lehetne még nyilvánvalób? 3 éve 0
-
Epyxoid: Tényleg annyi volna kazah, hogy ha a `D` az megegyezne az `F` csúccsal. Úgy tűnik tényleg megy valamennyire a matek sp! 3 éve 0
-
Epyxoid: Valóban van szó átlóról is, de a szögfelező és az átló nem ugyanaz... 3 éve 1
-
bazsa990608: Lehetséges hogy az átló felezi a szöget. Vagy nem tudom mire gondolhat vagy miféle feladat ez. 3 éve 0
-
segíítspls: Mert nem tudjátok értelmezni... 3 éve -1
-
Epyxoid: Ha úgy szólna a feladat, hogy "a `BF` az `ABE/_` szögfelezője", akkor volna arról szó, amit most mondasz. 3 éve 0
-
bazsa990608: Igen ezért mondom azt hogy túl sok olyan dolgot kéne magunktól felétételezni amit nem ad meg a feladat. 3 éve 0
-
bazsa990608: Az is lehetséges hogy maga a feladat leírása hibás. 3 éve 1
-
kazah: Igen, de sajnos nem egyezik meg a D pont az F csúccsal. A betűk tengerében elveszett a feladat. Mert Ez egy ABEF trapéz, nem pedig ABCD, a szöveg leírása közben azt hihette a kérdés feltevője, hogy az utóbbi; ugyanis ésszerűbb lenne egy trapézt így jelölni. 3 éve 1
-
Epyxoid: Mivel nem megoldható, így teljesen biztos, hogy erről van szó. Csak az a kérdés, hogy miért hibás? Lehet hiányos is, de lehet valamilyen elírás is. Viszont paraméteresen megoldható
 Ha elnevezzük a magasságot `x`-nek, akkor minden kifejezhető `x` függvényében!
Ha elnevezzük a magasságot `x`-nek, akkor minden kifejezhető `x` függvényében!  3 éve
0
3 éve
0
 Epyxoid
{ Tanár }
válasza
Epyxoid
{ Tanár }
válasza
Na tehát... Nevezzük a magasságot `x`-nek. Mindent ennek a függvényében fogunk megadni! (Azért `x` természetesen, mert ez a "főváltozónk", ami hiányzik a feladat leírásából, amivel egyértelműen megoldható lenne a feladat. Bármilyen más adatot is választhattam volna, de ez tűnt a legcélszerűbbnek, hiszen a magassága a második legmeghatározóbb adata egy trapéznak, persze erről lehetne vitatkozni. Illetve a levezetésem azt is bizonyítja, hogy az egész feladat minden kétséget kizáróan, egyértelműen megoldható volna pusztán ezen egyetlen egy további adat ismeretében!)
a)
Először is `x`-ből megkaphatjuk a másik szárat, a `b` oldalt, ugyanis ismerjük a `B` csúcsnál lévő szöget, amit én `alpha`-nak nevezek. Mivel a `BGE` egy derékszögű háromszöget alkot, erre felírhatjuk `alpha` szinuszát, ami
`sin alpha = x/b => b = x/(sin 60°) = x/(sqrt 3/2) = (2 sqrt 3)/3*x`
Ezután Pitagorasszal megkaphatjuk azt a szakaszt, amivel hosszabb a nagyalap a kisalaptól, amit én `d`-nek nevezek.
`x^2+d^2 = b^2 => d = sqrt(b^2-x^2) ``=`` sqrt( ((2 sqrt 3)/3*x)^2-x^2 ) ``=`` x sqrt( ((2 sqrt 3)/3)^2-1 ) ``=`` x sqrt(12/9-1) ``=`` sqrt 3/3*x`
Vagyis a `c` kisalap hossza:
`c = a-d = 15-sqrt 3/3*x`
b)
Na ez már egy kicsit cselesebb feladat, de nem kell túlságosan megijedni tőle. Fegyverünk, a derékszögű háromszögek gyártása mindennél erősebb! Például az `AF_(AB)C` egy derékszögű háromszög, aminek az oldalai `abs(AC)`, `x/2` és `a/2`, mivel a `C` pont a `BF` átló felezőpontja, vagyis felezi a magasságot, `x`-et és az alapot, `a`-t is. Tehát
`(a/2)^2+(x/2)^2 = abs(AC)^2 => abs(AC) = sqrt( (a/2)^2+(x/2)^2 ) ``=`` sqrt((225+x^2)/4) ``=`` sqrt(225+x^2)/2`
Hasonló módon a `CF_(GE)E` is derékszögű háromszög, aminek az oldalai `abs(CE)`, `x/2` és `a/2-d`. Az utóbbi könnyen belátható, hogyha az alapra eltoljuk a kérdéses oldalt (`CF_(GE)`), ami az `F_(AB)G` szakasz. Az `F_(AB)` megfelezi az `a` oldalt, a `GB` szakasz hossza pedig a `d`, vagyis az `F_(AB)G` hossza az `a/2-d`, vagyis a `CF_(GE)` hossza is ennyi. Nézzük ez valójában mit is jelent:
`a/2-d = 15/2-sqrt 3/3*x = 45/6-(2 sqrt 3 x)/6 = (45-2 sqrt 3 x)/6`
Tehát a `CE` hossza:
`(a/2-d)^2+(x/2)^2 = abs(CE)^2 => abs(CE) = sqrt( (a/2-d)^2+(x/2)^2 ) ``=`` sqrt( ((45-2 sqrt 3 x)/6)^2+x^2/4 ) ``=`` sqrt( (2025-180 sqrt 3 x+12x^2)/36+(9x^2)/36 ) ``=`` sqrt((2025-180 sqrt 3 x+21x^2)/36) ``=`` sqrt(2025-180 sqrt 3 x+21x^2)/6`
A legkönnyebb oldalt utoljára hagytam, hogy kicsit fellélegezhessünk! Egyébként nem is kell ezeket a kifejezéseket egyszerűbb alakra hozni, csak én szeretek velük elbabrálni. Utolsónak maradt az `e` oldal, ami a trapézunk másik átlója az `f` mellett, máskülönben. Ez az átló a trapéz "téglalap részét" felezi meg, amit két ugyanakkora derékszögű háromszögre oszt, az `AFE`-re és az `AGE`-re. Ezeknek az oldalai az `e`, az `x` és a `c`, ami ezt jelenti, hogy
Utolsónak maradt az `e` oldal, ami a trapézunk másik átlója az `f` mellett, máskülönben. Ez az átló a trapéz "téglalap részét" felezi meg, amit két ugyanakkora derékszögű háromszögre oszt, az `AFE`-re és az `AGE`-re. Ezeknek az oldalai az `e`, az `x` és a `c`, ami ezt jelenti, hogy
`c^2+x^2 = e^2 => e = sqrt(c^2+x^2) ``=`` sqrt((15-sqrt 3/3*x)^2+x^2) ``=`` sqrt(225-cancel 30_10*sqrt 3/cancel 3 x+1/3 x^2+3/3 x^2) ``=`` sqrt(225-10 sqrt 3 x+4/3 x^2)`
Vagyis végső soron a kerület:
`K_(ACE) = sqrt(225+x^2)/2 ``+`` sqrt(2025-180 sqrt 3 x+21x^2)/6 ``+`` sqrt(225-10 sqrt 3 x+4/3 x^2)`
Végszóként: Mivel a `D` pontot és vele együtt a szögfelezőt az egész feladat során sehol sem hasznosítottuk, tulajdonképpen üres, értelmetlen adat, azért sp ötlete nyomán hasznosítanám úgy, hogy feltesszük, hogy `D -= F`, tehát a szögfelező az maga a `BF` átló. Ekkor a következő adódik:
`x = a*"tg 30°" ``=`` cancel 15_5*sqrt 3/cancel 3 ``=`` 5 sqrt 3 ~~ "8,660 cm"`
`b = (2 sqrt 3)/3*5 sqrt 3 ``=`` (2*5*cancel 3)/cancel 3 ``=`` "10 cm"`
`d = sqrt 3/3*5 sqrt 3 ``=`` (5*cancel 3)/cancel 3 ``=`` "5 cm"`
`c = 15-5 ``=`` "10 cm"`
`(x^2 = (5 sqrt 3)^2 = 25*3 = 75)`
`abs(AC) = sqrt(225+75)/2 ``=`` sqrt 300/2 ``=`` (cancel 10_5 sqrt 3)/cancel 2 ``=`` 5 sqrt 3 ~~ "8,660 cm"`
`abs(CE) = sqrt(2025-180 sqrt 3*5 sqrt 3+21*75)/6 ``=`` sqrt(2025-2700+1575)/6 ``=`` sqrt 900/6 ``=`` 30/6 ``=`` "5 cm"`
`e = sqrt(225-10 sqrt 3*5 sqrt 3+4/3*75) ``=`` sqrt(225-150+100) ``=`` sqrt 175 ``=`` 5 sqrt 7 ~~ "13,229 cm"`
`K_(ACE) = 5 sqrt 3+5+5 sqrt 7 ``=`` 5(1+sqrt 3+sqrt 7) ~~ "26,889 cm"`
Ha bárkinek bármilyen kérdése felmerülne a feladattal kapcsolatban, arra nagyon szívesen válaszolok!
Köszönöm a figyelmet!
a)
Először is `x`-ből megkaphatjuk a másik szárat, a `b` oldalt, ugyanis ismerjük a `B` csúcsnál lévő szöget, amit én `alpha`-nak nevezek. Mivel a `BGE` egy derékszögű háromszöget alkot, erre felírhatjuk `alpha` szinuszát, ami
`sin alpha = x/b => b = x/(sin 60°) = x/(sqrt 3/2) = (2 sqrt 3)/3*x`
Ezután Pitagorasszal megkaphatjuk azt a szakaszt, amivel hosszabb a nagyalap a kisalaptól, amit én `d`-nek nevezek.
`x^2+d^2 = b^2 => d = sqrt(b^2-x^2) ``=`` sqrt( ((2 sqrt 3)/3*x)^2-x^2 ) ``=`` x sqrt( ((2 sqrt 3)/3)^2-1 ) ``=`` x sqrt(12/9-1) ``=`` sqrt 3/3*x`
Vagyis a `c` kisalap hossza:
`c = a-d = 15-sqrt 3/3*x`
b)
Na ez már egy kicsit cselesebb feladat, de nem kell túlságosan megijedni tőle. Fegyverünk, a derékszögű háromszögek gyártása mindennél erősebb! Például az `AF_(AB)C` egy derékszögű háromszög, aminek az oldalai `abs(AC)`, `x/2` és `a/2`, mivel a `C` pont a `BF` átló felezőpontja, vagyis felezi a magasságot, `x`-et és az alapot, `a`-t is. Tehát
`(a/2)^2+(x/2)^2 = abs(AC)^2 => abs(AC) = sqrt( (a/2)^2+(x/2)^2 ) ``=`` sqrt((225+x^2)/4) ``=`` sqrt(225+x^2)/2`
Hasonló módon a `CF_(GE)E` is derékszögű háromszög, aminek az oldalai `abs(CE)`, `x/2` és `a/2-d`. Az utóbbi könnyen belátható, hogyha az alapra eltoljuk a kérdéses oldalt (`CF_(GE)`), ami az `F_(AB)G` szakasz. Az `F_(AB)` megfelezi az `a` oldalt, a `GB` szakasz hossza pedig a `d`, vagyis az `F_(AB)G` hossza az `a/2-d`, vagyis a `CF_(GE)` hossza is ennyi. Nézzük ez valójában mit is jelent:
`a/2-d = 15/2-sqrt 3/3*x = 45/6-(2 sqrt 3 x)/6 = (45-2 sqrt 3 x)/6`
Tehát a `CE` hossza:
`(a/2-d)^2+(x/2)^2 = abs(CE)^2 => abs(CE) = sqrt( (a/2-d)^2+(x/2)^2 ) ``=`` sqrt( ((45-2 sqrt 3 x)/6)^2+x^2/4 ) ``=`` sqrt( (2025-180 sqrt 3 x+12x^2)/36+(9x^2)/36 ) ``=`` sqrt((2025-180 sqrt 3 x+21x^2)/36) ``=`` sqrt(2025-180 sqrt 3 x+21x^2)/6`
A legkönnyebb oldalt utoljára hagytam, hogy kicsit fellélegezhessünk! Egyébként nem is kell ezeket a kifejezéseket egyszerűbb alakra hozni, csak én szeretek velük elbabrálni.
 Utolsónak maradt az `e` oldal, ami a trapézunk másik átlója az `f` mellett, máskülönben. Ez az átló a trapéz "téglalap részét" felezi meg, amit két ugyanakkora derékszögű háromszögre oszt, az `AFE`-re és az `AGE`-re. Ezeknek az oldalai az `e`, az `x` és a `c`, ami ezt jelenti, hogy
Utolsónak maradt az `e` oldal, ami a trapézunk másik átlója az `f` mellett, máskülönben. Ez az átló a trapéz "téglalap részét" felezi meg, amit két ugyanakkora derékszögű háromszögre oszt, az `AFE`-re és az `AGE`-re. Ezeknek az oldalai az `e`, az `x` és a `c`, ami ezt jelenti, hogy`c^2+x^2 = e^2 => e = sqrt(c^2+x^2) ``=`` sqrt((15-sqrt 3/3*x)^2+x^2) ``=`` sqrt(225-cancel 30_10*sqrt 3/cancel 3 x+1/3 x^2+3/3 x^2) ``=`` sqrt(225-10 sqrt 3 x+4/3 x^2)`
Vagyis végső soron a kerület:
`K_(ACE) = sqrt(225+x^2)/2 ``+`` sqrt(2025-180 sqrt 3 x+21x^2)/6 ``+`` sqrt(225-10 sqrt 3 x+4/3 x^2)`
Végszóként: Mivel a `D` pontot és vele együtt a szögfelezőt az egész feladat során sehol sem hasznosítottuk, tulajdonképpen üres, értelmetlen adat, azért sp ötlete nyomán hasznosítanám úgy, hogy feltesszük, hogy `D -= F`, tehát a szögfelező az maga a `BF` átló. Ekkor a következő adódik:
`x = a*"tg 30°" ``=`` cancel 15_5*sqrt 3/cancel 3 ``=`` 5 sqrt 3 ~~ "8,660 cm"`
`b = (2 sqrt 3)/3*5 sqrt 3 ``=`` (2*5*cancel 3)/cancel 3 ``=`` "10 cm"`
`d = sqrt 3/3*5 sqrt 3 ``=`` (5*cancel 3)/cancel 3 ``=`` "5 cm"`
`c = 15-5 ``=`` "10 cm"`
`(x^2 = (5 sqrt 3)^2 = 25*3 = 75)`
`abs(AC) = sqrt(225+75)/2 ``=`` sqrt 300/2 ``=`` (cancel 10_5 sqrt 3)/cancel 2 ``=`` 5 sqrt 3 ~~ "8,660 cm"`
`abs(CE) = sqrt(2025-180 sqrt 3*5 sqrt 3+21*75)/6 ``=`` sqrt(2025-2700+1575)/6 ``=`` sqrt 900/6 ``=`` 30/6 ``=`` "5 cm"`
`e = sqrt(225-10 sqrt 3*5 sqrt 3+4/3*75) ``=`` sqrt(225-150+100) ``=`` sqrt 175 ``=`` 5 sqrt 7 ~~ "13,229 cm"`
`K_(ACE) = 5 sqrt 3+5+5 sqrt 7 ``=`` 5(1+sqrt 3+sqrt 7) ~~ "26,889 cm"`
Ha bárkinek bármilyen kérdése felmerülne a feladattal kapcsolatban, arra nagyon szívesen válaszolok!
Köszönöm a figyelmet!

Módosítva: 3 éve
0
-
segíítspls: Ne mivan mégis úgy kell megoldani ahogy mondtam? Meglepő..... 3 éve 0
-
segíítspls: De a nagy Kazah aaaaa nem lehet megoldni..... ha hülye vagy hozzá persze hogy nem.... 3 éve -2
-
Epyxoid: Tényleg az!
 Noha az túlzás, hogy "így kell megoldani", de valóban így van a legtöbb értelme, ezzel egyetértek. Viszont a feladatban továbbra sem ez áll.
3 éve
0
Noha az túlzás, hogy "így kell megoldani", de valóban így van a legtöbb értelme, ezzel egyetértek. Viszont a feladatban továbbra sem ez áll.
3 éve
0
-
Epyxoid: A feladatot abban a formájában ahogy meg van fogalmazva úgy csak paraméteresen lehet megoldani, mint ahogy meg is oldottam. Ahogy te megoldanád, hogy feltesszük, hogy el van írva a feladat, az már egy másik feladat, így kazahnak is nagyon is igaza volt. 3 éve 1
-
segíítspls: A feladatot mindíg úgy kell megoldni ahogy tudod hogy me legyen oldva azt csőőőőő 3 éve -1
-
Epyxoid: A feladat megoldhatósága érdekében élhetünk feltételezésekkel, de ezek csak feltételezések, a feladat nem határozta meg, így az eredeti feladat hibás, amit nem lehet csak úgy figyelmen kívül hagyni... 3 éve 0
-
Epyxoid: A matekban nincs helye a bizonytalanságoknak/feltételezéseknek. Azt kell megoldani, ami meg van határozva. Ami nincs, az nem létezik. 3 éve 0
-
segíítspls: Dehogynem ha nem lehet úgy megoldani megoldod másképp... Ha nem tudsz át ugorni 1 tankot nekifutásból akkor ki kerülöd.... 3 éve -1
-
Epyxoid: Ha az a feladat, hogy ugord át, akkor nem kerülheted meg. Pontosabban megkerülheted, de a feladatot - hogy átugord - azt nem teljesítetted... 3 éve 0
-
segíítspls: Az egész matematika feltételezésekre épült.... Ha ez Ha az 600 millió Ha míg betudták 1x bizonyítani. 3 éve -1
-
segíítspls: Hány olyan matek feladat van ahol feltételt kell írni pl egyenletek stb szóval deee elég sok feltételezésnek van helye. 3 éve -1
-
Epyxoid: Már hogy épülne feltételezésekre?
 A "ha" szót konkrét esetekkor használjuk. De általános esetekben nincs ha. Édes istenem.
3 éve
1
A "ha" szót konkrét esetekkor használjuk. De általános esetekben nincs ha. Édes istenem.
3 éve
1
-
Epyxoid: Arról nem beszélve, hogy a "feltétel" és a "feltételezés" az köszönő viszonyban sincs egymással... Kevered a szezont a fazonnal. 3 éve 1
-
kazah: Én is szeretlek, segíítspls
 De sajnos továbbra se látunk tőled semmit, szóval mégsem tudod megoldani. Egyébként a mindentudó titulus azt jelenti, hogy mindent tudok, még hibázni is
De sajnos továbbra se látunk tőled semmit, szóval mégsem tudod megoldani. Egyébként a mindentudó titulus azt jelenti, hogy mindent tudok, még hibázni is  Azzal a különbséggel, hogy én elismerem. De eddig és ezután sem hülyézek le senkit, ahogy te se tedd, inkább legyél építő jellegű.
3 éve
1
Azzal a különbséggel, hogy én elismerem. De eddig és ezután sem hülyézek le senkit, ahogy te se tedd, inkább legyél építő jellegű.
3 éve
1
-
segíítspls: Hogy vagy képes 1 mondaton belül ellent mondani saját magadnak? Gyakorlod? xddd 3 éve -1
-
Epyxoid: Naná. Mint te a levegőbe beszélést... Mindketten a mesterei vagyunk valaminek úgy látszik.
 3 éve
1
3 éve
1
-
segíítspls: Kazah elkezdted már tanulgatni a képleteket? xdddd 3 éve -2
-
bazsa990608: Őszintén sp én alig várom már a szeptembert hogy ismét rakosgasd fel a kis háziaid meg könyörögj üzenetekbe hogy segítsünk matekból, közgazdasából meg nemtudom már miből kértél mindíg segítséget. Szerintem ne számíts túl sok megoldásra a kérdéseid alatt. 3 éve 2
-
kazah: Segítettem már neked és te így hálálod meg? Szégyeld magad! 3 éve 1
-
segíítspls: Soha nem segítettél.... 3 éve -2
-
kazah: Itt bárki vissza tudja keresni, de egyébként itt vagyok már pár éve és futottam össze nálad nagyobb kötekedőkkel is, és sajnos ők mentek el innen, szóval tudod mi a sorsod, törődj bele
 Érdemes lesz másik játszóteret keresned magadnak.
3 éve
0
Érdemes lesz másik játszóteret keresned magadnak.
3 éve
0
-
Epyxoid: Egy percbe se tellett... https://ehazi.hu/q/112285 Nem szép ilyen gátlástalan módon hazudozni sp. Úgy csinálsz, mintha mindenki ellened volna itt, amikor te vagy itt mindenki ellen... 3 éve 1