Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Derékszögű háromszög
 Törölt
{ Kérdező } kérdése
Törölt
{ Kérdező } kérdése
419
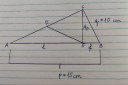
Mp magasságvonal 3:2 arányba osztja fel p szakaszt f és e szakaszra.
Határozd meg a háromszög területét, és hogy ADE háromszög hányad részét teszi ki a teljes háromszögnek.
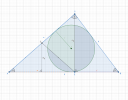
Számítsd ki a lehető legnagyobb háromszögbe írható kör területét és kerületét.
Számítsd ki DE és CE egyenesek mekkora részekre bontják a kör területét.
AD = DE
DE = DC
Határozd meg a háromszög területét, és hogy ADE háromszög hányad részét teszi ki a teljes háromszögnek.
Számítsd ki a lehető legnagyobb háromszögbe írható kör területét és kerületét.
Számítsd ki DE és CE egyenesek mekkora részekre bontják a kör területét.
AD = DE
DE = DC
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 Epyxoid
{ Tanár }
megoldása
Epyxoid
{ Tanár }
megoldása
`p = "15 cm", q = "10 cm"`
Én a harmadik oldalt akkor mondjuk `s`-nek nevezem el. Nem túl szerencsés a `p` és a `q`, mert azok általában párban vannak, de jó lesz így is.
Mivel tudjuk, hogy `e` és `f` milyen arányban osztja fel `p`-t, így ezek könnyen kiszámíthatók:
`e = p*3/(3+2) = cancel 15_3*3/cancel 5 = "9 cm"`
`f = p*2/5 = "6 cm"`
Majd észrevehetjük, hogy a `p` magasságvonala két derékszögű háromszögre osztja szét a háromszögünket, amikre felírhatjuk a Pitagoraszt:
`q^2 = m_p^2+f^2 => m_p = sqrt(q^2-f^2) = "8 cm"`
`s^2 = m_p^2+e^2 => s = sqrt(m_p^2+e^2) = sqrt 145 ~~ "12,042 cm"`
Vagyis a terület:
`T = (p*m_p)/2 = "60 cm"^2`
Mivel `AD = DC` és ezek együtt magát `s`-t teszik ki, így a hosszuk `s/2`. Tehát az `ADE` háromszög egy egyenlő szárú háromszög, aminek a szárai `s/2`, a harmadik oldala pedig `e`. Ha ezt megfelezzük függőlegesen a magassága mentén, akkor ismét derékszögű háromszögeket kapunk:
`(s/2)^2 = m_e^2+(e/2)^2 => m_e = sqrt(s^2/2^2-e^2/2^2) = sqrt((s^2-e^2)/4) = "4 cm"`
Tehát
`T_(ADE) = (e*m_e)/2 = "18 cm"`
A kettő aránya
`T_(ADE)/T = 18/60 = 3/10 = "0,3" = 30%`
A háromszögbe írható kör sugara a következőképpen adódik:
`r = (2T)/K`, ahol `T` a háromszög területe, `K` pedig a kerülete.
A területet már tudjuk. A kerület:
`K = p+q+s = 15+10+sqrt 145 ~~ "37,042 cm"`
Tehát
`r = (25-sqrt 145)/4 ~~ "3,240 cm"`
`T_r = r^2 pi ~~ "32,971 cm"^2`
`K_r = 2 pi r ~~ "20,355 cm"`
Az utolsó kérdés szerintem nem reális és eléggé kilóg a többi közül. Én ahogy elnézem elég gyötrődős lenne. Ha ti tanultatok erre valamilyen képletet, akkor kíváncsian várom mi lenne az, de máskülönben nem érné meg számolgatni, mert végső soron úgy se kérhetik ezt a részét számon, mert túl nehéz.
Várjunk csak. Most esik le, hogy az a kérdés címe, hogy "Derékszögű háromszög". De hisz a feladatban szereplő nem is egy derékszögű háromszög... Falnak futok.
Én a harmadik oldalt akkor mondjuk `s`-nek nevezem el. Nem túl szerencsés a `p` és a `q`, mert azok általában párban vannak, de jó lesz így is.
Mivel tudjuk, hogy `e` és `f` milyen arányban osztja fel `p`-t, így ezek könnyen kiszámíthatók:
`e = p*3/(3+2) = cancel 15_3*3/cancel 5 = "9 cm"`
`f = p*2/5 = "6 cm"`
Majd észrevehetjük, hogy a `p` magasságvonala két derékszögű háromszögre osztja szét a háromszögünket, amikre felírhatjuk a Pitagoraszt:
`q^2 = m_p^2+f^2 => m_p = sqrt(q^2-f^2) = "8 cm"`
`s^2 = m_p^2+e^2 => s = sqrt(m_p^2+e^2) = sqrt 145 ~~ "12,042 cm"`
Vagyis a terület:
`T = (p*m_p)/2 = "60 cm"^2`
Mivel `AD = DC` és ezek együtt magát `s`-t teszik ki, így a hosszuk `s/2`. Tehát az `ADE` háromszög egy egyenlő szárú háromszög, aminek a szárai `s/2`, a harmadik oldala pedig `e`. Ha ezt megfelezzük függőlegesen a magassága mentén, akkor ismét derékszögű háromszögeket kapunk:
`(s/2)^2 = m_e^2+(e/2)^2 => m_e = sqrt(s^2/2^2-e^2/2^2) = sqrt((s^2-e^2)/4) = "4 cm"`
Tehát
`T_(ADE) = (e*m_e)/2 = "18 cm"`
A kettő aránya
`T_(ADE)/T = 18/60 = 3/10 = "0,3" = 30%`
A háromszögbe írható kör sugara a következőképpen adódik:
`r = (2T)/K`, ahol `T` a háromszög területe, `K` pedig a kerülete.
A területet már tudjuk. A kerület:
`K = p+q+s = 15+10+sqrt 145 ~~ "37,042 cm"`
Tehát
`r = (25-sqrt 145)/4 ~~ "3,240 cm"`
`T_r = r^2 pi ~~ "32,971 cm"^2`
`K_r = 2 pi r ~~ "20,355 cm"`
Az utolsó kérdés szerintem nem reális és eléggé kilóg a többi közül. Én ahogy elnézem elég gyötrődős lenne. Ha ti tanultatok erre valamilyen képletet, akkor kíváncsian várom mi lenne az, de máskülönben nem érné meg számolgatni, mert végső soron úgy se kérhetik ezt a részét számon, mert túl nehéz.
Várjunk csak. Most esik le, hogy az a kérdés címe, hogy "Derékszögű háromszög". De hisz a feladatban szereplő nem is egy derékszögű háromszög... Falnak futok.

Módosítva: 3 éve
1
-
bazsa990608: Szép megoldás
 az utolsót én is irreálisan bonyoultnak találom egy ilyen feladathoz és túl macerás hogy bárhol feladják.
3 éve
1
az utolsót én is irreálisan bonyoultnak találom egy ilyen feladathoz és túl macerás hogy bárhol feladják.
3 éve
1
-
Epyxoid: Köszi! Igazándiból fejben végig sakkoztam, hogy koordináta geometriával nem volna annyira félelmetes (persze feleslegesen hosszadalmas volna), viszont ez nem egy koordinára geometriás feladat, így nem látom értelmét foglalkozni vele... 3 éve 0
-
Törölt: Köszönöm szépen 3 éve 1
-
Epyxoid: Szívesen! 3 éve 0