Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Tudnátok segíteni ebben a matematika feladatban?
 email1235
kérdése
email1235
kérdése
461
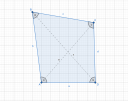
Egy általános négyszög 4 oldalát ismerjük, plusz a területét. Ezt szeretnénk felosztani két egyenlő területre, a d és a b oldal összekötésével, a kérdés, hogy ez a behúzott egyenesen milyen arányban osztja fel a b és a d oldalt.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
4 Epyxoid
{ Tanár }
válasza
Epyxoid
{ Tanár }
válasza
Hmm. Ott már egész jól kezdődik a dolog, hogy egy általános négyszögről van szó, viszont ez így önmagában nem megoldható, hiszen még csak annyit se tudunk, hogy egyáltalán konvex-e a négyszög, ami azért elég lényeges volna. Bár ezt leszámítva is egész kevés az adat, de ha legalább ez megvolna talán el lehetne indulni valahogy... Habár a területből talán ez indokolható... Hmm.
Módosítva: 3 éve
2
-
email1235: Igen én is ezen gondolkoztam, hogy kevés az adat, próbáltam valamit kiokoskodni, meg geogebrában is valahogy megszerkeszteni, de nagyon hiányzik legalább egy szög. 3 éve 0
-
Epyxoid: Nekem a szögek se segítenek
 Ki adta fel és miért? Tényleg felsőoktatásról származik a feladat?
3 éve
0
Ki adta fel és miért? Tényleg felsőoktatásról származik a feladat?
3 éve
0
 Epyxoid
{ Tanár }
válasza
Epyxoid
{ Tanár }
válasza
`T = "1112,9112 m"^2`
`a = "29,5237 m" ``", "`` b = "38,7173 m"`
`c = "34,0485 m" ``", "`` d = "32,6981 m"`
Talán a terület ismeretében el lehet indulni...
`T = sqrt( (p-a)(p-b)(p-c)(p-d)-abcd*cos^2((beta+delta)/2) ) ``", "`` p = (a+b+c+d)/2`
Ebből
`cos((beta+delta)/2) = sqrt( ((p-a)(p-b)(p-c)(p-d)-T^2)/(abcd) ) ~~ "0,161"`
`(beta+delta)/2 = cos^"-1"("0,161") ~~ "80,733°" => beta+delta ~~ "161,467°"`
Nevezzük ezt a szöget mondjuk `varphi`-nek, vagyis `varphi = beta+delta`.
Ekkor felírhatunk az átlókra egyenleteket, hátha abból kijön valami, ugyanis mindkét átló két-két általános háromszögre osztja ezt az alakzatot, amiknek ismerjük két szomszédos oldalát, a harmadik oldaluk közös (az átló maga), a két-két oldal által bezárt szögek összegét pedig most számoltuk ki. Legyen mondjuk az egyik átló `e`, a másik pedig `f`.
`e^2 = b^2+c^2-2bc*cos beta = a^2+d^2-2ad*cos(varphi-beta)`
`2bc*cos alpha - 2ad*cos(varphi-beta) = b^2+c^2-a^2-d^2`
Mivel tudjuk, hogy `cos(x-y) = cos x cos y + sin x sin y`, ezért
`2bc*cos beta - 2ad*(cos varphi cos beta + sin varphi sin beta) = b^2+c^2-a^2-d^2`
`(2bc-2ad cos varphi) cos beta - (2ad sin varphi) sin beta + (a^2-b^2-c^2+d^2) = 0`
`"...varázslat..."`
`beta_1 ~~ "73,022°" ", " cancel(beta_2 ~~ "271,334°")`, mivel `beta < varphi`
`delta ~~ "88,445°"`
`e ~~ "43,456 m"`
Ugyanez a másik átlóra is megcsinálható...
`alpha ~~ "97,314°"`
`gamma ~~ "101,220°"`
`f ~~ "51,592 m"`
Így legalább ábrázolni lehet a dolgokat, de közelebb nem vagyunk sajnos a megoldáshoz Érdekes feladat. Kíváncsi volnék a megoldására. Biztos valami tömör, lényegre törő képlet jönne ki végül a megoldásra, de nekem valahogy nem adja magát. Látom mindig hasonlóan extra nehéz feladatokat szoktál ide kitenni, email1235. Hát illik a többi közé ez is.
Érdekes feladat. Kíváncsi volnék a megoldására. Biztos valami tömör, lényegre törő képlet jönne ki végül a megoldásra, de nekem valahogy nem adja magát. Látom mindig hasonlóan extra nehéz feladatokat szoktál ide kitenni, email1235. Hát illik a többi közé ez is. 
`a = "29,5237 m" ``", "`` b = "38,7173 m"`
`c = "34,0485 m" ``", "`` d = "32,6981 m"`
Talán a terület ismeretében el lehet indulni...
`T = sqrt( (p-a)(p-b)(p-c)(p-d)-abcd*cos^2((beta+delta)/2) ) ``", "`` p = (a+b+c+d)/2`
Ebből
`cos((beta+delta)/2) = sqrt( ((p-a)(p-b)(p-c)(p-d)-T^2)/(abcd) ) ~~ "0,161"`
`(beta+delta)/2 = cos^"-1"("0,161") ~~ "80,733°" => beta+delta ~~ "161,467°"`
Nevezzük ezt a szöget mondjuk `varphi`-nek, vagyis `varphi = beta+delta`.
Ekkor felírhatunk az átlókra egyenleteket, hátha abból kijön valami, ugyanis mindkét átló két-két általános háromszögre osztja ezt az alakzatot, amiknek ismerjük két szomszédos oldalát, a harmadik oldaluk közös (az átló maga), a két-két oldal által bezárt szögek összegét pedig most számoltuk ki. Legyen mondjuk az egyik átló `e`, a másik pedig `f`.
`e^2 = b^2+c^2-2bc*cos beta = a^2+d^2-2ad*cos(varphi-beta)`
`2bc*cos alpha - 2ad*cos(varphi-beta) = b^2+c^2-a^2-d^2`
Mivel tudjuk, hogy `cos(x-y) = cos x cos y + sin x sin y`, ezért
`2bc*cos beta - 2ad*(cos varphi cos beta + sin varphi sin beta) = b^2+c^2-a^2-d^2`
`(2bc-2ad cos varphi) cos beta - (2ad sin varphi) sin beta + (a^2-b^2-c^2+d^2) = 0`
`"...varázslat..."`
`beta_1 ~~ "73,022°" ", " cancel(beta_2 ~~ "271,334°")`, mivel `beta < varphi`
`delta ~~ "88,445°"`
`e ~~ "43,456 m"`
Ugyanez a másik átlóra is megcsinálható...
`alpha ~~ "97,314°"`
`gamma ~~ "101,220°"`
`f ~~ "51,592 m"`
Így legalább ábrázolni lehet a dolgokat, de közelebb nem vagyunk sajnos a megoldáshoz
 Érdekes feladat. Kíváncsi volnék a megoldására. Biztos valami tömör, lényegre törő képlet jönne ki végül a megoldásra, de nekem valahogy nem adja magát. Látom mindig hasonlóan extra nehéz feladatokat szoktál ide kitenni, email1235. Hát illik a többi közé ez is.
Érdekes feladat. Kíváncsi volnék a megoldására. Biztos valami tömör, lényegre törő képlet jönne ki végül a megoldásra, de nekem valahogy nem adja magát. Látom mindig hasonlóan extra nehéz feladatokat szoktál ide kitenni, email1235. Hát illik a többi közé ez is. 
Módosítva: 3 éve
2
-
email1235: Az a baj, hogy ez nem konkrét feladat, csak egyik jó barátommal beszélgettünk és mondta, hogy van egy ilyen telek és, hogy elfelezik, aztán elkeztem rajta agyalni, hogy ez milyen jó matematikai probléma, csak elakadtam benne, azért tettem ki ide, hátha másokat is megfog ez a példa
 Már elfelezték valahogy, kiváncsi leszek, ha találkozunk milyen megoldás született ott
Már elfelezték valahogy, kiváncsi leszek, ha találkozunk milyen megoldás született ott  3 éve
1
3 éve
1
-
Epyxoid: Jaa, értem. Egyébként megoldható biztosan, de kva nehéz
 Amúgy átlehetne ültetni a problémát koordináta geometriába, ahol azért könnyebb dolgozni, de mit sem ér az egész, hogy ha nem tudjuk pontosan hogyan néz ki a telek, mert az én ábrámon az csak egy lehetséges alakzat, aminek ekkora a területe, de a szemben lévő szögek felcserélhetőek...
3 éve
0
Amúgy átlehetne ültetni a problémát koordináta geometriába, ahol azért könnyebb dolgozni, de mit sem ér az egész, hogy ha nem tudjuk pontosan hogyan néz ki a telek, mert az én ábrámon az csak egy lehetséges alakzat, aminek ekkora a területe, de a szemben lévő szögek felcserélhetőek...
3 éve
0
 Epyxoid
{ Tanár }
megoldása
Epyxoid
{ Tanár }
megoldása
Tovább gondoltam! Mivel ez nem egy matek probléma, hanem egy valóságos probléma, ezért nincs neki egy előre meghatározott megoldás menete, sőt a megoldásnak sem kell olyan végtelenül pontosnak lennie, így kitaláltam egy módot, amivel közelebb kerülhetünk a megoldáshoz...
Eredetileg az okozta a bonyodalmat nálam, hogy a szakasz, amit a `b` és `d` oldal összekötésével alkotunk, amivel megfelezzük a területet az lehet bármilyen meredekségű, és ezáltal bármilyen arányban megfelezheti az oldalakat, miközben továbbra is felezi a területet. Legalább is egy szabályos alakzatnál mindenképpen. Nem tudom, hogy egy ilyen szabálytalan alakzatra is érvényes-e ez az állítás, de meg mondom őszintén, nem adja magát nekem ez a kérdés, innen a fejfájás, amit okozott a feladat.
Viszont kiderült, hogy nem is érdekes, hogy milyen a dőlése ennek a szakasznak, a lényeg, hogy felezze a négyszöget, és innen az ötlet! Legyen párhuzamos ez a felező az alappal! Persze két alapunk is van, az `a` és a `c`, de az nem baj. Mindkettőre kiszámolhatjuk, hogy mi lenne az a velük párhuzamos egyenes, ami megfelezi a négyszöget és valahol félúton majd úgy is találkoznak és noha nem lesznek párhuzamosak - itt semmi sem párhuzamos -, de legalább így lesz egy elképzelésünk arról, hogy körülbelül merre is van ennek a förtelemnek a fele...
Kezdjük az elején! Nekem az `a` oldalán fekszik ez a síkidom, úgyhogy először ezt nézem. Egy olyan egyenest keresünk, ami párhuzamos az `a`-val és épp olyan messze van tőle, hogy felezze a területet. Ez az egyenes a négyszöget egy trapézzá hasítja szét, ami fenomenális, mivel annak sokkalta egyszerűbb a területe!
`T_"trapéz" = (a+c)/2 m`, ahol `a` és `c` a két alap, az `m` pedig a magasság.
Na most! Nekünk ebből csakis az egyik alap van meg, de nem kell félni, mert vannak szögeink! Nem tudom mennyire menjek bele a részletekbe, de zseniális az ötletem! Az az elgondolás, hogy egy trapéz lényegében olyan, mint egy négyzet, csak összetettebb. Tulajdonképpen mindegyik trapézban van egy négyzet, plusz a két oldalán két háromszög. Ezek a háromszögek pedig vagy hozzáadnak a területhez, hogy ha az alapon fekvő szögük nagyobb, mint 90° (kifelé nyílik az alakzat), vagy elvesznek belőle (befelé záródik az alakzat), attól függ melyik alapról nézzük. Egy szó, mint száz!
Az az elgondolás, hogy egy trapéz lényegében olyan, mint egy négyzet, csak összetettebb. Tulajdonképpen mindegyik trapézban van egy négyzet, plusz a két oldalán két háromszög. Ezek a háromszögek pedig vagy hozzáadnak a területhez, hogy ha az alapon fekvő szögük nagyobb, mint 90° (kifelé nyílik az alakzat), vagy elvesznek belőle (befelé záródik az alakzat), attól függ melyik alapról nézzük. Egy szó, mint száz!
`T/2 = ( 2a+m_a[ sin(alpha-90°) + sin(delta-90°) ] )/2 m_a`
Megdöbbentő, de sikerült egy olyan egyenletet gyártani, amiben csak egyetlen egy adat nem ismert, az `m_a`! Rendezzük is át rá az egyenletet!
`T = [sin(alpha-90°) + sin(delta-90°)]m_a^2 + 2am_a`
`[sin(alpha-90°) + sin(delta-90°)]m_a^2 + 2am_a - T = 0`
Ezzel kaptunk egy gyönyörű szép egyenletet `m_a`-ra. Lássuk mit ad ki!
`m_(a1) ~~ "18,2808 m", cancel(m_(a2) ~~ "-607,763")`, mivel `0 < m_a < e`
Illetve az alakzat másik felére is megcsinálhatjuk ugyanezt!
`T/2 = ( 2c+m_c[ sin(beta-90°) + sin(gamma-90°) ] )/2 m_c`
`[sin(beta-90°) + sin(gamma-90°)]m_c^2 + 2cm_c - T = 0`
`m_(c1) ~~ "16,7442 m", cancel(m_(c2) ~~ "682,103")`, mivel `0 < m_c < e`
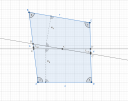
Az ábrán nagyon szépen látszik az eredmény! A két egyenes mind felezi az alakzatot és a `K` pontban metszik egymást. Tehát az `AD\D'A'` trapéz területe megegyezik a `BC\C'B'` trapéz területével, amik az egész négyszög területének felét teszik ki! Sajnos az értékek nem valami pontosak, már a szögek se voltak azok, így ezek a magasságok sem, de egész jó, még így is az eredmény. Az alkalmazás, amivel csinálom az ábrát `"556,627"`-et mond az `AD\D'A'` területére és `"555,121"`-et a `BC\C'B'` területére, úgyhogy a relatív hiba az kb `"0,241"%`, vagyis kevesebb, mint negyed százalék, ami azért nem szar...
Nézzük, hogy ez mit is jelent a `b` és `d` oldalakra nézve...
- Ha az `a` oldallal párhuzamosan felezünk:
`abs(A\A)' = m_a/cos(alpha-90°) ~~ "18,4307 m" ``", "`` abs(BA') ~~ "20,2866 m"`
`abs(D\D') = m_a/sin delta ~~ "18,2875 m" ``", "`` abs(CD') ~~ "14,4106 m"`
- Ha a `c` oldallal párhuzamosan felezünk:
`abs(B\B') = m_c/sin beta ~~ "17,5073 m" ``", "`` abs(AB') ~~ "21,2100 m"`
`abs(C\C') = m_c/cos(gamma-90°) ~~ "17,0704 m" ``", "`` abs(DC') ~~ "15,6277 m"`
Leírtam mindkét oldalról nézve a hosszakat, hogy oszlik meg a két oldal a két esetben. Mindkettő használható. Egyik az egyik egyirányú oldallal fut, a másik a másikkal és mindkettő felezi a területet! Bejelöltem az ábrámon az oldalfelezőket is, hogy lássuk mekkora az eltérés, hogy ha csak simán azok mentén szeljük ketté a négyszöget. Ebben az esetben a relatív hiba a területben kevesebb, mint 3%, így azért így se hibáztunk volna olyan nagyot. De hát azért még is csak, ennél 12-szer kisebb hiba is elérhető!
Bejelöltem az ábrámon az oldalfelezőket is, hogy lássuk mekkora az eltérés, hogy ha csak simán azok mentén szeljük ketté a négyszöget. Ebben az esetben a relatív hiba a területben kevesebb, mint 3%, így azért így se hibáztunk volna olyan nagyot. De hát azért még is csak, ennél 12-szer kisebb hiba is elérhető!  Illetve annyit még tegyünk hozzá, hogy nem biztos, hogy ugyanilyen elrendezésben vannak a szögek! A szemben lévő szögek felcserélhetőek tetszőlegesen a terület változása nélkül, így nem tudhatni, hogy pontosan hol melyik szög van...
Illetve annyit még tegyünk hozzá, hogy nem biztos, hogy ugyanilyen elrendezésben vannak a szögek! A szemben lévő szögek felcserélhetőek tetszőlegesen a terület változása nélkül, így nem tudhatni, hogy pontosan hol melyik szög van...
Eredetileg az okozta a bonyodalmat nálam, hogy a szakasz, amit a `b` és `d` oldal összekötésével alkotunk, amivel megfelezzük a területet az lehet bármilyen meredekségű, és ezáltal bármilyen arányban megfelezheti az oldalakat, miközben továbbra is felezi a területet. Legalább is egy szabályos alakzatnál mindenképpen. Nem tudom, hogy egy ilyen szabálytalan alakzatra is érvényes-e ez az állítás, de meg mondom őszintén, nem adja magát nekem ez a kérdés, innen a fejfájás, amit okozott a feladat.
Viszont kiderült, hogy nem is érdekes, hogy milyen a dőlése ennek a szakasznak, a lényeg, hogy felezze a négyszöget, és innen az ötlet! Legyen párhuzamos ez a felező az alappal! Persze két alapunk is van, az `a` és a `c`, de az nem baj. Mindkettőre kiszámolhatjuk, hogy mi lenne az a velük párhuzamos egyenes, ami megfelezi a négyszöget és valahol félúton majd úgy is találkoznak és noha nem lesznek párhuzamosak - itt semmi sem párhuzamos -, de legalább így lesz egy elképzelésünk arról, hogy körülbelül merre is van ennek a förtelemnek a fele...
Kezdjük az elején! Nekem az `a` oldalán fekszik ez a síkidom, úgyhogy először ezt nézem. Egy olyan egyenest keresünk, ami párhuzamos az `a`-val és épp olyan messze van tőle, hogy felezze a területet. Ez az egyenes a négyszöget egy trapézzá hasítja szét, ami fenomenális, mivel annak sokkalta egyszerűbb a területe!
`T_"trapéz" = (a+c)/2 m`, ahol `a` és `c` a két alap, az `m` pedig a magasság.
Na most! Nekünk ebből csakis az egyik alap van meg, de nem kell félni, mert vannak szögeink! Nem tudom mennyire menjek bele a részletekbe, de zseniális az ötletem!
 Az az elgondolás, hogy egy trapéz lényegében olyan, mint egy négyzet, csak összetettebb. Tulajdonképpen mindegyik trapézban van egy négyzet, plusz a két oldalán két háromszög. Ezek a háromszögek pedig vagy hozzáadnak a területhez, hogy ha az alapon fekvő szögük nagyobb, mint 90° (kifelé nyílik az alakzat), vagy elvesznek belőle (befelé záródik az alakzat), attól függ melyik alapról nézzük. Egy szó, mint száz!
Az az elgondolás, hogy egy trapéz lényegében olyan, mint egy négyzet, csak összetettebb. Tulajdonképpen mindegyik trapézban van egy négyzet, plusz a két oldalán két háromszög. Ezek a háromszögek pedig vagy hozzáadnak a területhez, hogy ha az alapon fekvő szögük nagyobb, mint 90° (kifelé nyílik az alakzat), vagy elvesznek belőle (befelé záródik az alakzat), attól függ melyik alapról nézzük. Egy szó, mint száz!`T/2 = ( 2a+m_a[ sin(alpha-90°) + sin(delta-90°) ] )/2 m_a`
Megdöbbentő, de sikerült egy olyan egyenletet gyártani, amiben csak egyetlen egy adat nem ismert, az `m_a`! Rendezzük is át rá az egyenletet!
`T = [sin(alpha-90°) + sin(delta-90°)]m_a^2 + 2am_a`
`[sin(alpha-90°) + sin(delta-90°)]m_a^2 + 2am_a - T = 0`
Ezzel kaptunk egy gyönyörű szép egyenletet `m_a`-ra. Lássuk mit ad ki!
`m_(a1) ~~ "18,2808 m", cancel(m_(a2) ~~ "-607,763")`, mivel `0 < m_a < e`
Illetve az alakzat másik felére is megcsinálhatjuk ugyanezt!
`T/2 = ( 2c+m_c[ sin(beta-90°) + sin(gamma-90°) ] )/2 m_c`
`[sin(beta-90°) + sin(gamma-90°)]m_c^2 + 2cm_c - T = 0`
`m_(c1) ~~ "16,7442 m", cancel(m_(c2) ~~ "682,103")`, mivel `0 < m_c < e`
Az ábrán nagyon szépen látszik az eredmény! A két egyenes mind felezi az alakzatot és a `K` pontban metszik egymást. Tehát az `AD\D'A'` trapéz területe megegyezik a `BC\C'B'` trapéz területével, amik az egész négyszög területének felét teszik ki! Sajnos az értékek nem valami pontosak, már a szögek se voltak azok, így ezek a magasságok sem, de egész jó, még így is az eredmény. Az alkalmazás, amivel csinálom az ábrát `"556,627"`-et mond az `AD\D'A'` területére és `"555,121"`-et a `BC\C'B'` területére, úgyhogy a relatív hiba az kb `"0,241"%`, vagyis kevesebb, mint negyed százalék, ami azért nem szar...
Nézzük, hogy ez mit is jelent a `b` és `d` oldalakra nézve...
- Ha az `a` oldallal párhuzamosan felezünk:
`abs(A\A)' = m_a/cos(alpha-90°) ~~ "18,4307 m" ``", "`` abs(BA') ~~ "20,2866 m"`
`abs(D\D') = m_a/sin delta ~~ "18,2875 m" ``", "`` abs(CD') ~~ "14,4106 m"`
- Ha a `c` oldallal párhuzamosan felezünk:
`abs(B\B') = m_c/sin beta ~~ "17,5073 m" ``", "`` abs(AB') ~~ "21,2100 m"`
`abs(C\C') = m_c/cos(gamma-90°) ~~ "17,0704 m" ``", "`` abs(DC') ~~ "15,6277 m"`
Leírtam mindkét oldalról nézve a hosszakat, hogy oszlik meg a két oldal a két esetben. Mindkettő használható. Egyik az egyik egyirányú oldallal fut, a másik a másikkal és mindkettő felezi a területet!
 Bejelöltem az ábrámon az oldalfelezőket is, hogy lássuk mekkora az eltérés, hogy ha csak simán azok mentén szeljük ketté a négyszöget. Ebben az esetben a relatív hiba a területben kevesebb, mint 3%, így azért így se hibáztunk volna olyan nagyot. De hát azért még is csak, ennél 12-szer kisebb hiba is elérhető!
Bejelöltem az ábrámon az oldalfelezőket is, hogy lássuk mekkora az eltérés, hogy ha csak simán azok mentén szeljük ketté a négyszöget. Ebben az esetben a relatív hiba a területben kevesebb, mint 3%, így azért így se hibáztunk volna olyan nagyot. De hát azért még is csak, ennél 12-szer kisebb hiba is elérhető!  Illetve annyit még tegyünk hozzá, hogy nem biztos, hogy ugyanilyen elrendezésben vannak a szögek! A szemben lévő szögek felcserélhetőek tetszőlegesen a terület változása nélkül, így nem tudhatni, hogy pontosan hol melyik szög van...
Illetve annyit még tegyünk hozzá, hogy nem biztos, hogy ugyanilyen elrendezésben vannak a szögek! A szemben lévő szögek felcserélhetőek tetszőlegesen a terület változása nélkül, így nem tudhatni, hogy pontosan hol melyik szög van...
Módosítva: 3 éve
1
-
email1235: köszönöm szépen
 egy két ilyen való életben lévő problémánál jövök rá mindig, hogy milyen szép a matematika
egy két ilyen való életben lévő problémánál jövök rá mindig, hogy milyen szép a matematika  3 éve
1
3 éve
1
-
Epyxoid: Érdekes probléma az biztos! Nagyon szívesen!
 3 éve
0
3 éve
0