Nekem ebből nem derül ki, hogy hogyan van megvágva a kör. Még ha párhuzamosan is vágunk 3 centire egymástól, még akkor is lehet bárhol a körön belül az a két vágás.

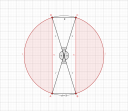
Fogalmam sincs hogy jó e de én speciel így értelmeztem a kérdést. Aztán kiderül hogy a többiek milyen meglátáson vannak.
A kép erősen torzított képet ad csak az elképzelés érdekében csináltam.

Én a vágások távolságát `d`-vel, a sugarat `r`-rel, a vágások húrját `c`-vel, a hozzájuk tartozó köríveket pedig `i`-vel jelölöm.

a)
A kör területéből először is kiszámolhatjuk a sugarát.
`T = r^2 pi => r = sqrt(T/pi) = sqrt(80/pi) = 4 sqrt(5/pi) ~~ "5,046 cm"`

Ezek után mondjuk a szögeket volna jó megtudni. Szerencsére az `ABO` (az ábrán) egy olyan háromszöget alkot, aminek ismert mindegyik oldala, vagyis a koszinusztétellel kiszámolható `beta`.
`d^2 = r^2+r^2-2rr*cos beta ``=>`` cos beta = (2r^2-d^2)/(2r^2) = (160-9 pi)/160 ``=>`` beta = cos^"-1"((160-9 pi)/160) ~~ "34,585°"`

Amiből `alpha`:
`alpha = 180° - beta ~~ "145,415°"`

A körszelet területét ezek után úgy kaphatjuk meg, hogy a hozzátartozó körcikkből kivonjuk azt a háromszöget, amiben eltér a körszelet a körcikktől. Az ábrán például a baloldali körszelet területét úgy kapjuk, hogy ha az `AOD` körcikk területéből kivonjuk az `AOD` háromszög területét.

Egy körcikk területe úgy aránylik a teljes kör területéhez, ahogy a hozzátartozó középponti szög a teljes szöghöz. Tehát
`T_"körcikk"/T_"kör" = alpha/(360°) ``=>`` T_"körcikk" = r^2 pi * alpha/(360°) ~~ "32,314 cm"^2`
A háromszög területe pedig kiszámolható két oldal és a közrezárt szögük szinuszával:
`T_(/_\\) = (rr sin alpha)/2 ~~ "7,227 cm"^2`

Tehát a körszelet területe:
`T_"körszelet" = T_"körcikk" - T_(/_\\) ~~ "25,087 cm"^2`
Ha mindkettő kell, akkor az ennek a kétszerese:
`2*T_"körszelet" ~~ "50,174 cm"^2`

b)
A vágás után kapott síkidom területe a következőképpen adódik:
`T_"vágott kör" = T-2*T_"körszelet" ~~ 80-"50,174" = "29,826 cm"^2`

A kerület már kicsit összetettebb ennél. Az eredeti kör kerületéből le kell vonni a körszeletekhez tartozó körívet (`i`) és hozzáadni a hozzátartozó húrok hosszát (`c`). A húr hasonlóan alakul, mint a körcikk. A húr hossza úgy aránylik a teljes kerülethez, mint a hozzátartozó szög a teljesszöghöz. Azaz
`i/(2 pi r) = alpha/(360°) => i = 2 pi r*alpha/(360°) ~~ "12,807 cm"`

A `c` húr pedig mondjuk kiszámolható a koszinusztétellel, mint ahogy `beta`-t is kiszámoltuk, csak itt most a szög megvan (`alpha`) és most az oldal nincs meg.
`c^2 = r^2+r^2-2rr*cos alpha ``=>`` c = sqrt(2r^2(1-cos alpha)) ~~ "9,636 cm"`

Ami azt jelenti, hogy
`K_"vágott kör" = K - 2i + 2c = 2 pi r - 2(i+c) = 2(pi r-i+c) ~~ "25,365 cm"`