Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Pótvizsga második rész 2. Feladat
Törölt
kérdése
214
Egy hétszög köré írt kör Kerülete = 450 cm.
Számítsd ki a hétszög oldalait.
Számítsd ki a leghosszabb átlót.
Számítsd ki a legrövideb átlót.
Számítsd ki mekkora szöget szár be a leghosszabb és legrövidebb átló egymáshoz képest.
Számítsd ki a hétszög oldalait.
Számítsd ki a leghosszabb átlót.
Számítsd ki a legrövideb átlót.
Számítsd ki mekkora szöget szár be a leghosszabb és legrövidebb átló egymáshoz képest.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2
kazah
megoldása
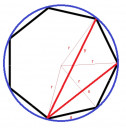
A kör kerülete 450 cm.
A kör sugara: r = `K/(2*pi)` = `450/(2*3.14)` = 71,62 cm.
A középponti szögek `360/7`° és ennek többszörösei lesznek.
Az oldal kiszámításához használjuk a koszinusztételt:
`a^2=r^2+r^2-2*r*r*cosalpha` , ahol `alpha=360/7`
`a=r*root()(2)*root()(1-cosalpha)` = `71.62*1.41*root()(1-cos(360/7))` `approx` 61,96 cm
Rövid átló:
`x=r*root()(2)*root()(1-cos(2*alpha))` = `71.62*1.41*root()(1-cos(2*360/7))` `approx` 111,66 cm
Hosszú átló:
`y=r*root()(2)*root()(1-cos(3*alpha))` = `71.62*1.41*root()(1-cos(3*360/7))` `approx` 139,23 cm
A közbezárt szög: A három oldalhossz alapján szintén koszinusztétellel számoljuk a szöget:
Az x és y oldal által bezárt szög:
`a^2=x^2+y^2-2*x*y*cosalpha`
`cosalpha=(x^2+y^2-a^2)/(2*x*y)` = `(111.66^2+139.23^2-61.96^2)/(2*111.66*139.66)` = 0,9
`alpha` = 25,71°.
Ábra
A kör sugara: r = `K/(2*pi)` = `450/(2*3.14)` = 71,62 cm.
A középponti szögek `360/7`° és ennek többszörösei lesznek.
Az oldal kiszámításához használjuk a koszinusztételt:
`a^2=r^2+r^2-2*r*r*cosalpha` , ahol `alpha=360/7`
`a=r*root()(2)*root()(1-cosalpha)` = `71.62*1.41*root()(1-cos(360/7))` `approx` 61,96 cm
Rövid átló:
`x=r*root()(2)*root()(1-cos(2*alpha))` = `71.62*1.41*root()(1-cos(2*360/7))` `approx` 111,66 cm
Hosszú átló:
`y=r*root()(2)*root()(1-cos(3*alpha))` = `71.62*1.41*root()(1-cos(3*360/7))` `approx` 139,23 cm
A közbezárt szög: A három oldalhossz alapján szintén koszinusztétellel számoljuk a szöget:
Az x és y oldal által bezárt szög:
`a^2=x^2+y^2-2*x*y*cosalpha`
`cosalpha=(x^2+y^2-a^2)/(2*x*y)` = `(111.66^2+139.23^2-61.96^2)/(2*111.66*139.66)` = 0,9
`alpha` = 25,71°.
Ábra
1
- Még nem érkezett komment!
kazah
válasza
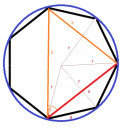
Mivel két leghosszabb átló van, így a másikat is be lehet rajzolni és kiszámolni, ekkor
`cosbeta=(y^2+x^2-x^2)/(2*x*y)` = `(139.23^2)/(2*111.66*139.23)` = 0,62
`beta` = 51,41°
`cosbeta=(y^2+x^2-x^2)/(2*x*y)` = `(139.23^2)/(2*111.66*139.23)` = 0,62
`beta` = 51,41°
1
-
kazah: Mármint egy csúcsból húzható két leghosszabb átló
1 éve
0
-
Epyxoid: Igen. Egy csúcsból két rövid és két hossz átló húzható, amik között van egy kisebb és egy nagyobb szög. Szép levezetés. Jó gyorsan megoldottad! 1 éve 0