Keresés


Toplista

Toplista
  • betöltés...

Magántanár kereső

Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!

Pótvizsga első felének 2. feladata

179
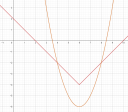
Ábrázold a két függvényt és határozd meg hol metszik egymást!
f(x)= (x-6)² - harmadik gyök alatt √64 * 27
g(x)= abszolút értékben x - 6 abszolút érték bezár - 4
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika

Válaszok

2
Csatoltam képet.
Remélem jól értelmeztem ezek a leírások alapján.
Biztosan lesz aki jobban elmagyarázza nekem nem a magyarázás az erősségem.
Válasz kép
Válasz kép
Módosítva: 1 éve
4


Az ábrázolásnál (bár ezt iskolája válogatja) szokták így leírni:

Függvénytranszformációk:

I. `y=x^2` alapfüggvény

II. `y=(x-6)^2` eltolás az x tengely mentén pozitív irányba 6 egységgel

III. `y=(x-6)^2-6` eltolás az y tengely negatív irányba 6 egységgel.

Azt tudjuk, hogy mikor lesz felfelé nyíló parabola (ha a négyzetes tag előjele pozitív)

A szélsőértékkel kezdd, a (0;0) lesz eltolva 6 egységgel jobbra és 6 egységgel lefelé, a többit ahogy Bazsa írta.

Az abszolútértékesnél szintén hasonlók a függvénytranszformációk:

I. `y=|x|` alapfüggvény

II. `y=|x-6|` eltolás az x tengely mentén pozitív irányba 6 egységgel

III. `y=|x-6|-4` eltolás az y tengely mentén negatív irányba 4 egységgel.

Az alapfüggvényt itt is a (0;0) pontból érdemes indítani, ott van a függvény szélsőértéke, így a V betű csúcsa a (6;-4) pont lesz, a többi fentebb.

Módosítva: 1 éve
2