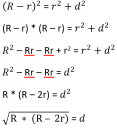Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Pótvizsga (titkos feladat)
 Törölt
kérdése
Törölt
kérdése
560
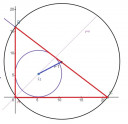
Egy derékszögű háromszög két befogója 16 és 21 cm. Határozd meg a beírt és a köré írt kör középpontjának távolságát.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
4 bazsa990608
{ Közgazdász }
megoldása
bazsa990608
{ Közgazdász }
megoldása
Csatoltam képet.
5
-
Ármós Csaba: Ügyesek vagytok kazah-hal!
 3 éve
3
3 éve
3
-
kazah: Bazsa nélkülem is ügyes

 3 éve
4
3 éve
4
-
segíítspls: Honnan jöttek ezek a képletek? Szerintem csak ki találtad.. 3 éve -4
-
Epyxoid: Szerintem titokban súgtál neki kazah, ne szerénykedj
 (csak viccelek!!)
3 éve
2
(csak viccelek!!)
3 éve
2
-
kazah: Én amúgyis később válaszoltam, én lestem innen, de a távolságosat azt nem ismertem (persze gondolom le lehet vezetni). 3 éve 4
-
bazsa990608: Erre eszek egyet hogy Kazahnak is tudtunk újat mutatni Epyxoid

 3 éve
2
3 éve
2
-
Epyxoid: Ennyi! Bár inkább csak te, mert én már rég elfelejtkeztem róla
 De nézd meg, rögtön megoldja másképpen még ilyenkor is!
3 éve
2
De nézd meg, rögtön megoldja másképpen még ilyenkor is!
3 éve
2
-
kazah: Ja, az én megoldásom ilyen fapados módszer, ha nem tudsz valami képletet, akkor kerüld ki
 Amúgy nekem is sok új van, a jelmondatom: Matekórát adok-veszek
Amúgy nekem is sok új van, a jelmondatom: Matekórát adok-veszek  3 éve
3
3 éve
3
-
kazah: Vagy még ez jöhet szóba: 1. Hiányoztam, amikor tanították. 2. Nem tanították, mert még már olyan öreg vagyok (na annyira azért nem) 3. Elfelejtettem
 Eulerről egyébként elsőnek az `e^(i*pi)+1=0` ugrik be. Másodiknak meg a `pi` kiszámítása a négyzetszámok reciprokösszegével. De annyi mindennel foglalkozott, hogy nem csoda, ha nem ismerjük minden tételét.
3 éve
3
Eulerről egyébként elsőnek az `e^(i*pi)+1=0` ugrik be. Másodiknak meg a `pi` kiszámítása a négyzetszámok reciprokösszegével. De annyi mindennel foglalkozott, hogy nem csoda, ha nem ismerjük minden tételét.
3 éve
3
-
Törölt: Köszönöm szépen
 3 éve
2
3 éve
2
 kazah
válasza
kazah
válasza
Egy koordináta-geometriai megoldás:
Legyen a háromszög:
A(0;0), B(0;16) és C(21;0). (Ábra)
Ekkor:
A háromszög köré írható kör középpontjának koordinátái az átfogó felezőpontja.
`F_1`: `(21/2;16/2)` = `(10.5;8)`
A beírható kör középpontja rajta van a derékszög szögfelezőjén; tehát annak ordinátája és abszcisszája megegyezik; sugara számítható (ahogy bazsa is tette):
`T=r*s` = `r*K/2`
T = `(16*21)/2` = 168 `cm^2`
s = `(16+21+root()(16^2+21^2))/2` = 31,7 cm
r = `T/s` = `168/31.7` = 5,3 cm
A beírható kör középpontjának koordinátái tehát:
`F_2` : (5,3;5,3)
A két pont távolsága:
`d(F_1-F_2)` = `root()((x_(F1)-x_(F2))^2+(y_(F1)-y_(F2))^2)` = `root()((10.5-5.3)^2+(8-5.3)^2)` `approx` 5,86 cm
Legyen a háromszög:
A(0;0), B(0;16) és C(21;0). (Ábra)
Ekkor:
A háromszög köré írható kör középpontjának koordinátái az átfogó felezőpontja.
`F_1`: `(21/2;16/2)` = `(10.5;8)`
A beírható kör középpontja rajta van a derékszög szögfelezőjén; tehát annak ordinátája és abszcisszája megegyezik; sugara számítható (ahogy bazsa is tette):
`T=r*s` = `r*K/2`
T = `(16*21)/2` = 168 `cm^2`
s = `(16+21+root()(16^2+21^2))/2` = 31,7 cm
r = `T/s` = `168/31.7` = 5,3 cm
A beírható kör középpontjának koordinátái tehát:
`F_2` : (5,3;5,3)
A két pont távolsága:
`d(F_1-F_2)` = `root()((x_(F1)-x_(F2))^2+(y_(F1)-y_(F2))^2)` = `root()((10.5-5.3)^2+(8-5.3)^2)` `approx` 5,86 cm
5
-
segíítspls: Full érthetetlen.... 3 éve -4
-
kazah: Az nem szégyen, csak kellemetlen
 3 éve
1
3 éve
1
-
Epyxoid: Szóval az `R` hosszát ki se számolod, mi? Nagyon cseles!
 3 éve
2
3 éve
2
-
kazah: Ha már úgyis két pont távolsága kell, akkor nem erőltettem
 3 éve
2
3 éve
2
-
Epyxoid: Persze világos. Teljesen jó! Amúgy a beírt kör képlete nélkül is kiszámolható lenne a távolság a terület és a kerület nélkül, most hogy így belegondolok. Csak a `c` oldal metszéspontja kell `y=x`-szel és annak a fele a középpont.. 3 éve 1
-
Epyxoid: Áhh, csak szeretném! De tényleg kiszámítható lenne így is, csak nem a fele lesz, hanem az `(1+(sqrt 2)/2)`-ede! 3 éve 0
-
Törölt: Köszönöm szépen 3 éve 0
 Epyxoid
{ Tanár }
válasza
Epyxoid
{ Tanár }
válasza
Ide szegődnék én is harmadiknak... Nincs már sok minden, amit hozzátehetnék a megoldáshoz, de azért mégis csak, hátha segít...
Igazából ide csak képleteket kell tudni...
A beírt kör sugarának hossza:
`r = (2T)/K = T/s`
A köré írt kör sugarának hossza:
`R = (abc)/(4T)`
A kettő középpontjának távolsága `x`, pedig
`x = sqrt(R(R-2r)) = sqrt(R^2-2Rr)`
ahol `a, b, c` a háromszög oldalai, `T` a területe, `K` a kerülete, és `s` a kerület fele.
Ezek voltak az általános képletek. Viszont itt, mivel ez egy derékszögű háromszög, ezért a terület képlet egyszerűsödik egy általános háromszögéhez képest.
`T = (a*b)/2`
ahol `a, b` a háromszög két befogója.
Tehát:
`r = (2*(ab)/2)/K = (ab)/(a+b+c) ``", "`` R = (abc)/(4*(ab)/2) = c/2`
A `c` oldal Pitagorasz tételéből adódik, mivel derékszögű a háromszög:
`a^2+b^2=c^2 ``=>`` c = sqrt(a^2+b^2) = sqrt(16^2+21^2) = sqrt 697 ~~ "26,401 cm"`
`r = (16*21)/(16+21+sqrt 697) = (37-sqrt 697)/2 ~~ "5,300 cm" ``", "`` R = (sqrt 697)/2 ~~ "13,200 cm"`
Vagyis
`x = sqrt(((sqrt 697)/2)^2 - 2*(sqrt 697)/2*(37-sqrt 697)/2) = sqrt(2091 - 74 sqrt(697))/2 ~~ "5,860 cm"`
Ha bármi kérdésed felmerülne nyugodtan tedd fel. Szívesen válaszolok rá!
Igazából ide csak képleteket kell tudni...
A beírt kör sugarának hossza:
`r = (2T)/K = T/s`
A köré írt kör sugarának hossza:
`R = (abc)/(4T)`
A kettő középpontjának távolsága `x`, pedig
`x = sqrt(R(R-2r)) = sqrt(R^2-2Rr)`
ahol `a, b, c` a háromszög oldalai, `T` a területe, `K` a kerülete, és `s` a kerület fele.
Ezek voltak az általános képletek. Viszont itt, mivel ez egy derékszögű háromszög, ezért a terület képlet egyszerűsödik egy általános háromszögéhez képest.
`T = (a*b)/2`
ahol `a, b` a háromszög két befogója.
Tehát:
`r = (2*(ab)/2)/K = (ab)/(a+b+c) ``", "`` R = (abc)/(4*(ab)/2) = c/2`
A `c` oldal Pitagorasz tételéből adódik, mivel derékszögű a háromszög:
`a^2+b^2=c^2 ``=>`` c = sqrt(a^2+b^2) = sqrt(16^2+21^2) = sqrt 697 ~~ "26,401 cm"`
`r = (16*21)/(16+21+sqrt 697) = (37-sqrt 697)/2 ~~ "5,300 cm" ``", "`` R = (sqrt 697)/2 ~~ "13,200 cm"`
Vagyis
`x = sqrt(((sqrt 697)/2)^2 - 2*(sqrt 697)/2*(37-sqrt 697)/2) = sqrt(2091 - 74 sqrt(697))/2 ~~ "5,860 cm"`
Ha bármi kérdésed felmerülne nyugodtan tedd fel. Szívesen válaszolok rá!
Módosítva: 3 éve
5
-
kazah: Még esetleg az nem lehet világos, hogy a két pont távolsága `x=root()(R(R-2r))`. Benne van a függvénytáblázatban vagy egy általánosan elfogadott képlet? Ezzel még nem találkoztam, azért csináltam inkább koordinátásan. 3 éve 2
-
bazsa990608: Ez a képlet az Euler tétel rendezett változata. Igen hivatalosan elfogadott képlet. (R - r)2 = r2 + d2 rendezve pontosan ezt adja ki. d a két középpont távolságát jelenti. 3 éve 2
-
kazah: Oké, köszi
 3 éve
1
3 éve
1
-
Epyxoid: Ezért is mondtam, hogy ez a feladat inkább csak képlet magolás, mint intuíció. Nyilván már a sugarak képletét se tudnám megindokolni. A két középpont távolsága nem tudom benne van-e a fv táblázatban, de rémlik, hogy tanultuk/tanítják, úgyhogy szerintem idevág. Amúgy a wikipediáról szedtem
 3 éve
1
3 éve
1
-
Epyxoid: Fúú, valami nagyon halványan dereng... Ezerszázalék, hogy tanultam középsuliba, de meg nem mondanám hogy jön ki... Euler-nek meg több tétele van a matematikában, mint ahány betű létezik az összes nyelvben együttvéve
 3 éve
1
3 éve
1
-
Törölt: Köszönöm szépen 3 éve 1
 bazsa990608
{ Közgazdász }
válasza
bazsa990608
{ Közgazdász }
válasza
Maga a képlet rendezve így jön ki.
7
-
Epyxoid: Azta, nagyon köszönöm! Viszont `d`-re rendezni még csak-csak menne nekem is
 Én azt nem tudom, hogy ez első sor honnan ered. Ha arról tudsz valamilyen olvasmányt mutatni, akkor azt szívesen elolvasgatom
Én azt nem tudom, hogy ez első sor honnan ered. Ha arról tudsz valamilyen olvasmányt mutatni, akkor azt szívesen elolvasgatom  3 éve
1
3 éve
1
-
bazsa990608: Hát én még a suliba tanultam annó de ezt találtam https://hu.m.wikipedia.org/wiki/Euler-t%C3%A9tel_(geometria) 3 éve 2
-
Epyxoid: De jóóó! Köszönöm szépen!!! 3 éve 0
-
kazah: Köszi!
 3 éve
0
3 éve
0