a)
Mivel egyenlő szárú a háromszögünk - mivel két oldala egyenlő hosszú, ez legyen mondjuk `b` -, ezért a velük szemközti szögek is egyenlőek, vagyis az `A` és `B` csúcsnál lévő szögek. Ez legyen mondjuk az `alpha` szög. A `C` csúcsnál lévő meg mondjuk a `gamma`. (Mert azért mégse a `beta` legyen a `C` csúcsnál.) Az ismeretlen oldal pedig legyen `a`.

Mivel tudjuk, hogy a `hat(DBA)` az 15°, és mivel az `ABD` egy derékszögű háromszöget alkot, ezért az `alpha = 75°`, de ezt már te is kiszámoltad. Viszont tovább mehetünk, ugyanis ekkor tudjuk, hogy a `B` csúcsnál lévő szög is ugyanennyi. A `gamma` pedig 180°-ra egészíti ki a belső szögek összegét, vagyis `gamma = 180-2 alpha = 30°`

b)
A kerülethez kell mind a 3 oldal hossza, viszont eddig csak 2 oldalt ismerünk. A harmadik oldal kiszámítására használhatjuk mondjuk a szinusztételt: (de a koszinusztételt is)
`a/b = sin gamma/sin alpha => a = b*sin gamma/sin alpha = 8*sin(30°)/sin(75°) = 4 sqrt 6-4 sqrt 2 ~~ "4,141 cm"`

Tehát a kerület:
`K = a + 2 b = 4 sqrt 6-4 sqrt 2 + 16 ~~ "20,141 cm"`

c)
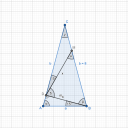
Itt arra jutottam, hogy az a legegyszerűbb, hogy ha kiszámoljuk a `DBM` háromszög szögeit és majd azok segítségével jutunk a `DM` szakasz hosszának nyomára, amit `x`-nek nevezek. Ezeket a szögeket mind el is neveztem, `beta`-nak, `delta`-nak és `mu`-nek, az ábrán látszik melyik melyik.

Mivel tudjuk, hogy az `ABD` háromszög `B` csúcsánál lévő szög az `alpha` és hogy a `hat(DBA) = 15°`, ezért
`beta = alpha-15 = 60°`
Hasonló módon, mivel tudjuk, hogy a `hat(BDC)` az derékszög és az `hat(MDC)` az 15°, ezért
`delta = 90-15 = 75°`
Az utolsó szög, pedig
`mu = 180 - beta - delta = 180-60-75 = 45°`
Innentől már csak egy kicsit kell szenvedni!

Az `ABD` háromszögre felírhatjuk az `alpha` szinuszát, ami
`sin alpha = m_b/a => m_b = a sin alpha = b sin gamma = "4 cm"`

A `BDM` háromszögre pedig felírhatjuk újfent a szinusztételt:
`x/m_b = sin beta/sin mu`

Vagyis végül:
`x = m_b*sin beta/sin mu = 4*sin(60°)/sin(45°) = 2 sqrt 6 ~~ "4,899 cm"`