Geometriai gyakorló feladat amiben elakadtam.

Mik ezek a nehéz feladatok? Hova jársz a Harvardra? Már a kérdést se értik az emberek.....

a)
Csinálom a többit is (de azokat már táblán hogy legyen elég hely), de mint minden megoldásnál itt is megvan rá az esély hogy belekavarodtam valamibe

b) Itt is fent áll a hiba lehetősége mint mindig

c)

d) térfogatos része
Nem tudom hogy miért tartott eddig
Mondjuk lehet nem jó, de szerintem valahogy így néz ki, csinálom a területes részét is

És ha minden igaz akkor ez a területváltozás (ami egyébként +6,99 cm^2 ha jól számoltam)
Ezt meg az előző feladatot a kúpra nézve oldottam meg.

No összegezzük akkor, hogy pontosan miből is állna megoldani ezt a feladatot, mert noha érkezett két megoldás is, amik ugyan jók, de az egyik túlságosan tagolt, a másik pedig pont hogy túl rövid, kevés levezetéssel. Én megpróbálok a kettő között alkotni valamit. Remélem sikerül! Persze magamat ismerve hosszú lesz...

Én az alapélt `a`-val, az oldalélt pedig `o`-val jelölöm.

a)
Ennek a gúlának a felszínét ugyanúgy kapjuk, mint bármelyikét: az oldalainak területének összeg. Ez a mi esetünkben az alap területe, plusz a 6 db oldallapé, amik a palástot alkotják.
`F_"gúla" = T_"alap" + 6*T_"oldal"`

Az alaplap területe egy szabályos hatszög, vagyis 6 db egyenlő oldalú `/_\\`-ből áll, amiknek az oldala 8 cm. Ezeknek a magassága kéne és akkor a területük `T_/_\\ = (a*m_a)/2`, az alaplapé pedig `T_"alap" = 6*T_/_\\`. A magasság pedig könnyen adódik, mivel ha megfelezzük ezt a `/_\\`-et, akkor egy derékszögű háromszöget kapunk (1. ábra), aminek ismert két oldala, a harmadik pedig a magasság, vagyis használható Pitagorasz tétele:
`a^2 = m_a^2 + (a/2)^2`
`m_a = sqrt(a^2-(a/2)^2) = sqrt (8^2 - 4^2) = sqrt 48 = 4 sqrt 3 ~~ "6,928 cm"`
Tehát
`T_"alap" = 6*((cancel 8_4*4 sqrt 3)/cancel 2) = 96 sqrt 3 ~~ "166,277 cm"^2`

A palást felszínének, vagyis a 6 db oldallapnak a területének a kiszámítása is rettentő hasonló lesz. Tulajdonképpen csak annyi a különbség, hogy az oldallapoknak más lesz a magassága, de egyébként pontosan így adódik az is. Ha egy oldallapot (ami egy egyenlő szárú háromszög) vágunk függőlegesen félbe, akkor megint csak derékszögű háromszögeket kapunk, amiknek a az átfogója az oldalél, a két befogója pedig `a/2` és a keresett magasság (2. ábra). Vagyis
`o^2 = m_o^2 + (a/2)^2`
`m_o = sqrt(o^2-(a/2)^2) = sqrt(10^2-4^2) = sqrt 84 = 2 sqrt 21 ~~ "9,165 cm"`
Tehát
`T_"oldal" = (cancel 8_4*2 sqrt 21)/cancel 2 = 8 sqrt 21 ~~ "36,661 cm"^2`

Vagyis a gúla felszíne:
`F_"gúla" = 96 sqrt 3 + 6*(8 sqrt 21) = 48(2 sqrt 3 + sqrt 21) ~~ "386,241 cm"^2`

A térfogat már valamivel egyszerűbb, ugyanis egy gúla (vagy kúp ha kör alapú) térfogata az alapterület szorozva a magassággal osztva 3-mal minden esetben. A magasságot én `h`-nak keresztelem.
`V_"gúla" = (T_"alap"*h)/3`

Ebből újfent egy magasságot nem ismerünk, ami ez úttal a `h` nevet viseli, de ugyanúgy fogjuk kiszámolni, mint az előző kettőt: keresünk egy derékszögű háromszöget, aminek az egyik oldala ez a magasság, a másik kettőt pedig már ismerjük. Ehhez talán kell egy kis térlátás, és vagy fantázia, de ami azt illeti kettő ilyen háromszög is van! Ha oldalról nézzük az alakzatot, amit majd megint csak megfelezünk függőlegesen, akkor forgathatjuk úgy az alakzatot, hogy az alaplap egyik háromszögének magassága `m_a`, az oldallap magassága `m_o` és a keresett magasság `h` alkot egy derékszögű háromszöget. De nem csak így, az oldalfelezők mentén vizsgálhatjuk a dolgot, hanem az egyik csúcs és a hozzátartozó él mentén is, amikor is az `a`, az `o` és a `h` alkot egy derékszögű háromszöget (3. ábra). Ezek közül mindkettő jó megoldást ad. Én az utóbbit választom, mert azok kerekebb értékűek. A másik eshetőség házi feladat!
Tehát
`o^2 = h^2 + a^2`
`h = sqrt(o^2-a^2) = sqrt(10^2-8^2) = sqrt 36 = "6 cm"`

Ami azt jelenti, hogy a gúla térfogata:
`V_"gúla" = (96 sqrt 3*cancel 6_2)/cancel 3 = 192 sqrt 3 ~~ "332,554 cm"^3`

b)
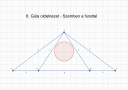
Itt nem tudom mennyire szorul magyarázatra, hogy melyik a legnagyobb alapterületű kör, ami a szabályos hatszögbe írható. Adja magát igazából. Ennek a sugara egyenlő a hatszöget hat részre osztó háromszögek magasságával, `m_a`-val (4. ábra). Vagyis
`r -= m_a = 4 sqrt 3 ~~ "6,928 cm"`

A kúp felszíne hasonló a gúláéhoz, csak itt most a palást nem oldallapokból áll, hanem egyetlen folyamatos alakzatból (amit ha kiterítenénk egy síkra akkor egy körcikket formálna mellesleg), ami egy kicsit megnehezíti a dolgunkat, de valójában mégsem, mert a képlet egészen egyszerű. Ehhez szükség van az alkotó hosszához, amit egyenlőre `u`-nak nevezek el.
`F_"kúp" = T_"alap" + P = r^2 pi + r u pi`

Az `u`, az alkotó az a hossz, távolság, ami összeköti a kör alapot a csúcs ponttal. Ezt az értéket már ismerjük, mert a gúlában is szerepel. A 4-es ábrán látható, hogy milyen pontokban érintkezik a gúla a kúppal és hol pedig nem. Például a gúla csúcsainál és oldaléleinél nem, viszont az oldalfelezőknél érintkezik, ami azt jelenti, hogy itt ráfekszik a gúla a kúpra. Tehát a kúp alkotója nem más, mint a gúla oldallapjának magassága!
`u -= m_o = 2 sqrt 21 ~~ "9,165 cm"`

Miután ezt beláttuk a kúp felszíne könnyen adódik:
`F_"kúp" = (4 sqrt 3)^2 pi + 4 sqrt 3*2 sqrt 21*pi = 48 pi + 24 pi sqrt 7 = 24 pi (2+sqrt 7) ~~ "350,281 cm"^2`

A térfogata pedig:
`V_"kúp" = ((4 sqrt 3)^2 pi*cancel 6_2)/cancel 3 = 96 pi ~~ "301,593 cm"^3`

c) `V_"kúp"/V_"gúla" = (cancel 96 pi)/(cancel 192_2 sqrt 3) = pi/(2 sqrt 3) ~~ "90,690"%`

d)
Na ez nagy falat lesz... Mindenek előtt kössük ki, hogy a gúlába éppen az oldalfelezők mentén fúrtunk bele, amit semmi nem köt ki, de enélkül konkrétan értelme nincs a feladatnak, mert a furat térfogata és felülete is változik attól függően, hogy milyen szögben fúrjuk meg a gúlát. Nyilván a kúpnál nem számít, mert az egy forgástest.

Először a térfogatokra koncentrálnék. A gúla esete könnyebb, sőt az a legegyszerűbb a négy közül, szóval azzal kezdem. Tehát a lyuk átmérője `d`, a furat pedig egy kör alapú hasábból, azaz hengerből áll, aminek a két vége "le van vágva" ahogy véget ér a gúla az oldallapjainál (5. ábra). Tehát `J_0`-tól `J_1`-ig teljes egészében a testben halad a furat, majd `J'_1`-től `L_1`-ig egy "vágott hengerrel" végződik a furat. Viszont ha ehhez a `L_1J_1J'_1` végződéshez hozzáadjuk a másik oldalit (`L_2J_2J'_2`), akkor pont egy teljes hengert alkotnak, aminek a hossza `L_1J_1` hossza, vagyis olyan, mintha a furat `K_1`-től `K_2`-ig egy teljes henger lenne. `K_1K_2` hossza legyen `l`.
Mivel `IF_(AB)G ∼ IK_1K_0`, ezért
`(F_(AB)G)/(GI) = (K_1K_0)/(K_0I)`, vagyis
`m_a/h = (l/2)/(h/2) = l/h => l = m_a`

Tehát a furat térfogata a gúla esetén:
`V_"furat" = T_○*l = (d^2 pi)/4*l = (9 pi)/cancel 4*cancel 4 sqrt 3 = 9 pi sqrt 3 ~~ "48,973 cm"^3`
`V_"lyukas gúla" = V_"gúla"-V_"furat" = 192 sqrt 3 - 9 pi sqrt 3 = (192-9 pi) sqrt 3 ~~ "283,581 cm"^3`

A kúp esete viszont már nem ilyen egyszerű. A különbség a 4. ábrából látszik a legtisztábban, felül nézetből. Mivel az `F_(AB)` vonalában fúrtunk, így odaképzelhetjük a fúrószár hegyét. Ha csak egy nagyon kicsi lukat fúrnánk, vagyis ha `F_(AB)`-től csak kis távolságra vagyunk, akkor az `AB` oldal és a körív szinte alig tér el. Az `A`, `B` csúcsoknál pedig a legnagyobb az eltérés. Sajnos ez az eltérés koránt sem egységes és a pontos értékének kiszámítása jelen esetben legalább egy hármas integrál kiszámításával lenne kivitelezhető, amitől én elhatárolnám magam. Helyette amit korábban kiszámoltunk, a kúp és a gúla térfogatának arányát veszem alapul. Ezzel fogom beszorozni a furat azon részét, ami már részben a testen kívül van, vagyis a két végét. Ehhez ki kell számolni, hogy milyen hosszú a furat teljes henger része, vagyis a `J_1J_0` szakasz hossza. Elég kacifántos lenne megindokolni miért annyi amennyi. Nem húznám vele az időt. Pont fele az `l`-nek, amivel előbb számoltunk. Egy szó, mint száz (amúgy se hiszem, hogy lényeges a feladat ezen része; képtelenség, hogy ilyen feladatot kapj élesben a suliban, plusz ez amúgy is már csak egy közelítés):
`V_"kúp furat" ~~ T_○*l/2 + T_○*l/2*V_"kúp"/V_"gúla" = (9 pi sqrt 3)/2 + (9 pi cancel sqrt 3)/2*pi/(2 cancel sqrt 3) = (18 pi sqrt 3 + 9 pi^2)/4 ~~ "46,693 cm"^3`
Ez a fenti egy felső becslést ad az eltérésre, vagyis több eltéréssel számol a valósnál, vagyis a valós érték még ennél is kevésbé tér el a gúlánál kapottnál, ami vicc. Szinte semmis a különbség...
`V_"lyukas kúp" ~~ V_"kúp"-V_"kúp furat" = 96 pi - (18 pi sqrt 3 + 9 pi^2)/4 ~~ "254,900 cm"^3`

Na a poén ebben az egész d) pontban, hogy már a térfogatokat is teljesen szopás végigvezetni. Erre amikor úgy vagy vele, hogy letudtad, akkor még hátra vannak a felszínek, amik egy teljesen eltérő problémával szolgálnak, amik ugyanolyan nehezek, mint a térfogatok... Nem reális ez az alfeladat. Ami reális lehet, mint válasz, hogy a fúrást követően, a térfogatok csökkennek, a felszínek pedig növekednek ugye és ennyiben ki is merül a térfogatok és felszínek változásának mibenléte. Ennél pontosabb választ nem várhatnak el középiskolában. Még egyetemen sem kegyetlenek annyira, hogy ilyen feladatokat adjanak fel, mert semmi tanulságuk nincs. Na de lássuk... Most járunk pontosan a feladat felénél máskülönben. Őrület.

A felszín változás megint csak a gúla esetében kezelhetőbb, sőt, a kúp esete is ebből volna származtatható, ha egyáltalán volna értelme számszerűsíteni a dolgot, szóval lássuk a gúla esetét. Mivel a furat kör alapú, a gúla oldala viszont szögben áll ezzel, ezért a gúla oldallapján a furat körének a vetülete látszik majd, amit egyedül az oldal dőlésszöge határoz majd meg (5. ábra). Ez a vetület egy ellipszis lesz, lényegében az eredeti kör függőlegesen megnyújtva. Az, hogy mennyivel nyúlik meg arra én is csak intuitíve jöttem rá, így azt bizonyítani nem tudom és a magyarázkodással sem bajlódnék, a lényeg, hogy az oldal dőlésszögének szinuszának reciprokával nyúlik meg a kör. (Egyébként ebből sikerült rájönnöm: https://www.geogebra.org/m/fxjypmny#material/ck6jydp2 ) Ezek után a terület is egész szerencsésen adódik, mert tulajdonképpen csak ezzel a megnyúlással kell az eredeti területet beszorozni, ami az ellipszisek terület képletéből adódik. Vagyis a felszín a következőképpen alakul:

`F_"lyukas gúla" = F_"gúla" - 2*T_"ellipszis" + P_"furat"`, ahol `T_"ellipszis" = (d^2 pi)/4*1/sin varphi`

A `varphi` szerencsére viszonylag egyszerűen adódik. Ha az `F_(AB)GI` háromszöget nézzük, akkor ott `varphi` szinusza az épp a szemközti befogó `h`, osztva az átfogóval, ami az `m_o`. Tehát `sin varphi` nem más, mint
`sin varphi = h/m_o = cancel 6_3/(cancel 2 sqrt 21) = 3/sqrt 21`
Azaz
`T_"ellipszis" = (cancel 9_3 pi)/4*sqrt 21/cancel 3 = (3 pi sqrt 21)/4 ~~ "10,797 cm"^2`

A furat palástjának kiszámításakor pedig ugyanazt a cselt bevethetjük, mint amit a tréfogat számításkor is, vagyis a henger vágott két vége együtt egy egész henger palástot ad, vagyis egyenértékű a valódi furatot egy `l` hosszú teljes hengerként kezelni. Ennek a palástja:
`P_"furat" = d pi*l = 3 pi*4 sqrt 3 = 12 pi sqrt 3 ~~ "65,297 cm"^2`

Tehát az új felszín:
`F_"lyukas gúla" = 48(2 sqrt 3 + sqrt 21) - cancel 2*(3 pi sqrt 21)/cancel 4_2 + 12 pi sqrt 3 = (8+pi) 12 sqrt 3 + (48-3/2 pi) sqrt 21 ~~ "429,942 cm"^2`

A kúp esetében a furat kör alakú vetülete tovább torzul, ugyanis most már nem egy síkra vetül, hanem egy íves felületre. Viszont amivel ez a torzulás megnöveli ezt a felületet annyival csökken a furat palástjának a felülete, úgyhogy valamennyire kiüti egymást az eltérés a gúlához képest. Mivel alapból is a teljes felszín csupán töredékéről beszélünk a furat esetében, ez az eltérés pedig ennek a töredéknek is a töredéke, így én nyugodt szívvel tekintenék el tőle, de ha a tanárod ad a megoldáshoz megoldókulcsot, akkor marha kíváncsi vagyok ott hogyan számolják ki. Vagyis az új kúp felszín nagyjából:
`F_"lyukas kúp" ~~ F_"kúp" - 2*T_"ellipszis" + P_"furat" = 24 pi (2+sqrt 7) - (3 pi sqrt 21)/2 + 12 pi sqrt 3 ~~"393,983 cm"^2`

Összegezve a d) pontot: hogy ha csakis a gúla változásait kérdezték volna, akkor egy indokolatlanul szemét feladat lenne az egész, ami megfelelően érdekes és kihívásokkal teli. Viszont a kúp változásainak kiszámolása teljesen abszurd kérés, amihez hasonlóval úgy sem kell soha az életben bajlódnod, így ez a része a feladatnak egyáltalán nem reális. Sőt, ez már egy olyan jellegű problémakör, amit vissza lehetne szegezni a tanárnak, aki feladta és le merném fogadni, hogy belátható időn belül ő sem tudná megoldani.

Testvérem lemodellezte nekem a kúp esetét, amit nem tudtam pontosan kiszámolni, csak közelíteni, így megvannak a pontos értékek:
`V_"lyukas kúp" = V_"kúp"-V_"kúp furat" ~~ 96 pi - "47,736" = "253,856 cm"^3,` `varepsilon_(r%) = "0,409" %`
`F_"lyukas kúp" = F_"kúp" - 2*T_"kúp furat vég" + P_"kúp furat" ~~ 24 pi (2+sqrt 7) - 2*"11,117" + "61,857" = "389,904 cm"^2,` `varepsilon_(r%) = "1,035" %`

Láthatjuk, hogy míg a térfogatnál próbáltam jobb közelítést adni a magoldásra, így ott csak fél százalék a hiba, a felszínnél pedig nem, ott csak a gúlánál számoltakkal számoltam módosítás nélkül, de még így is csak 1% lett a relatív hiba... Ergó, nem igazán éri meg a vesződést a kúp esetével bíbelődni... Ha a gúla adataival dolgozunk, amik számíthatóak, még úgy is 1%-os a hiba nagyság rendje, ami még egy egyszerű kerekítési hibával is összemérhető, ha nem vigyáz az ember.

Itt van pár kép a modellről: https://imgur.com/a/b9kp5UC