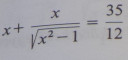Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Újabb egyenlet
 yhrufcg5
kérdése
yhrufcg5
kérdése
459
Oldja meg a valós számok halmazán az alábbi egyenletet!
Jelenleg 1 felhasználó nézi ezt a kérdést.
egyenlet
egyenlet
2
Középiskola / Matematika
Válaszok
6 zalavaribotond
{ Elismert }
válasza
zalavaribotond
{ Elismert }
válasza
Ha minden igaz akkor ez jó lesz:
Ha kell levezetem hogy hogyan lett 4 eredmény de mivel ilyen feladatokat kaptok szerintem az nem szorul magyarázatra hogy x×x×x2 miért x4
De remélem nem nagy baj hogy az nincsen papíron mind a 4 x-re
Ha kell levezetem hogy hogyan lett 4 eredmény de mivel ilyen feladatokat kaptok szerintem az nem szorul magyarázatra hogy x×x×x2 miért x4
De remélem nem nagy baj hogy az nincsen papíron mind a 4 x-re
Módosítva: 3 éve
0
-
yhrufcg5: Az nem szorul magyarázatra, az viszont igen, hogy ez a sárga csíkos feladatgyűjteményben van és 1998-as kiadás, az érdekelne, hogy hogyan kell egy ilyen feladatot megoldani papíron. A negyedfokú egyenletekkel még nehezen boldogulok. 896-os feladat, ha ez segít. Az egyenletmegoldó programokat én is ismerem, ötből kettő meg is tudja oldani. 3 éve 2
-
zalavaribotond: Több módszerrel is meg lehet őket oldani, pl ott van a grafikus módszer tehát ábrázolod őket. A negyed fokú egyenlet alatt az ax^4+bx^3+cx^2+dx+e=0-ra gondolsz? Mert azokat én sem tudom fejből 3 éve 0
-
zalavaribotond: Ha pl ilyenekre gondolsz mint amit most is csináltam akkor pl kihozod olyan alakra hogy x^4+x^2+c=0, azután x^2helyére behelyettesíted y-t. De várjál inkább ezt is megcsinálom papíron, egyszerűbb lesz úgy 3 éve 0
 zalavaribotond
{ Elismert }
válasza
zalavaribotond
{ Elismert }
válasza
Így gondoltam, és mint írtam különböző egyéb módszerekkel lehet még módosítani az egyenlete (nyilván úgy hogy a kifejezés értéke ne változzon meg)
Egyébként ez a hivatalos negyedfokú:
https://hu.wikipedia.org/wiki/Negyedfok%C3%BA_egyenlet
De szerintem nincs olyan ember a világon aki ezt képes lenne bemagolni anélkül hogy értse. Bár statisztikailag biztosan van legalább egy
Egyébként ez a hivatalos negyedfokú:
https://hu.wikipedia.org/wiki/Negyedfok%C3%BA_egyenlet
De szerintem nincs olyan ember a világon aki ezt képes lenne bemagolni anélkül hogy értse. Bár statisztikailag biztosan van legalább egy
Módosítva: 3 éve
0
-
yhrufcg5: Igen, ezt tudom, másodfokúra visszavezethető egyenlet. De a konkrét példában ezt nehezen lehet megcsinálni, a gyökök ismerete nélkül pedig nehéz eldönteni, hogy milyen harmad- vagy elsőfokú taggal bővítsünk. 3 éve 1
-
kazah: Na igen, ha ilyen egyszerű lenne a harmad vagy negyedfokú egyenlet, akkor nem lenne fél mérföldes a megoldóképlet...
 3 éve
2
3 éve
2
-
zalavaribotond: Sajnos erre egyedül a gyakorlás van mint opció, vagy egy jó matektanár akivel hasonló feladatokat csinálsz majdnem minden órán 3 éve 0
-
zalavaribotond: Na várjál 3 éve 0
-
zalavaribotond: Levezettem 3 éve 0
 zalavaribotond
{ Elismert }
válasza
zalavaribotond
{ Elismert }
válasza
Nem a legjobb a képminőség, de azért olvasható, ez az eredménye annak ha jó vagy az összefüggések felismerésében, kiemelésben meg ha a matektanárod a nézésével ölni tud. Meg ha nincs életed és nyáron is matekozol meg fizikázol mert az jobban érdekel mint a szociális élet... Na de mindegy is
0
-
zalavaribotond: Remélem ez így jó levezetés lett 3 éve 0
-
Epyxoid: Számomra felfoghatatlan, hogy mennyire jól tudsz szorzatra alakítani!
 3 éve
0
3 éve
0
-
zalavaribotond: Minden matek tanáromnál az volt a befutó hogy mit miből lehet kiemelni így hát ehhez szoktam hozzá 3 éve 0
 Epyxoid
{ Tanár }
válasza
Epyxoid
{ Tanár }
válasza
Azért jó az értelmezési tartománnyal foglalkozni az ilyen feladatokban, mert - egyrészt jó gyakorlás, másrészt - az közvetlenül megindokolja nekünk, hogy melyik kapott megoldás elégíti ki az eredeti egyenletet és melyik nem. Az értelmezési tartományt olyan dolgok szűkíthetik, mint például hogy a nevező nem lehet nulla, a gyök alatti kifejezés nem lehet negatív, illetve a gyökös kifejezés egy oldalra rendezése után a másik oldal sem lehet negatív, hiszen maga a gyökös kifejezés sem lehet az. Tehát tudjuk, hogy
`x^2-1 > 0`
`x^2 > 1 " /" sqrt`
`abs x > 1 => x in (-oo, -1) uu (1, oo)`
Illetve majd amikor lejjebb egy oldalra rendezem a gyökös kifejezést, abból láthatjuk, hogy mi marad az egyenlet másik oldalán, ami nem lehet negatív. Vagyis
`(12x)/(35-12x) >= 0`
Egy tört akkor nagyobb, mint 0, ha a számlálója és nevezője vagy nagyobb, vagy kisebb, mint 0. Nulla pedig akkor lehet, ha a számláló nulla, de a nevező nem nulla. Tehát:
`I.`
`{(12x >= 0, => x >= 0), (35-12x > 0, => x < 35/12):}`
`=> 0 <= x < 35/12 => x in [0, 35/12)`
`II.`
`{(12x <= 0, => x <= 0), (35-12x < 0, => x > 35/12):}`
`=> 35/12 < x <= 0 => x in O/`
Ezeket összegezve pedig azt kapjuk, hogy az értelmezési tartomány a következő:
`D = (1, 35/12) = (1; "2,91"dot 6)`
(Ezzel zárom majd ki a megoldások felét később!)
Most, hogy ez megvolt lássunk neki a feladatnak!
`(x)/sqrt(x^2-1) = 35/12-x` `" /" *12 sqrt(x^2-1)`
`12x = (35-12x)*sqrt(x^2-1)` `" /" :(35-12x)`
`(12x)/(35-12x) = sqrt(x^2-1)` `" /" ()^2`
`((12x)/(35-12x))^2 = x^2-1`
`(144x^2)/(35-12x)^2 = x^2-1` `" /" *(35-12x)^2`
`144x^2 = (x^2-1)(35-12x)^2`
`144x^2 = (x^2-1)(1225-840x+144x^2)`
`144x^2 = 1225x^2-840x^3+144x^4 - 1225+840x-144x^2`
`144x^4 - 840x^3 + 937x^2 + 840x - 1225 = 0`
Már eddig eljutni is elég szopás volt... Ami most jön csak még inkább az lesz! Tudjuk, hogy `144x^4=(12x^2)^2`, illetve hogy `1225 = 35^2`, de mivel 35 az `5*7`, ezért `35^2 = (5*7)^2 = 5^2*7^2 = 25*49`. Tehát valami ilyenre jó lenne szétbontani a fentit:
`(12x^2 + Ax + 25)*(12x^2 + Bx - 49)`
`144x^4 + 12Bx^3 - 12*49x^2 + 12Ax^3 + ABx^2 - 49Ax + 12*25x^2 + 25Bx - 1225`
`144x^4 + (12B+12A)x^3 + (-12*49+AB+12*25)x^2 + (-49A+25B)x - 1225`
Ezt a mi egyenletünkkel összevetve a következőt kapjuk:
`{("I.", 12A+12B = -840),("II.", AB+12(25-49) = 937),("III.", 25B-49A = 840):}`
A II.-on dolgozhatunk egy kicsit:
`AB-12*24 = 937`
`AB = 1225`
Illetve adja magát, hogy `-"III." = "I."`, tehát:
`12A+12B = 49A - 25B` `" /" -12A+25B`
`37A = 37B`
`A = B`
Ezt visszahelyettesítve az elsőbe megkapjuk, hogy
`A = B = -35`
Vagyis a szorzatunk nem más, mint:
`(12x^2 - 35x + 25)*(12x^2 - 35x - 49) = 0`
Innentől pedig már jelentősen könnyebb a dolgunk:
`I.`
`12x^2 - 35x + 25 = 0`
`x_1 = 5/4 = "1,25";` `x_2 = 5/3 = "1,6"dot 6`
`II.`
`12x^2 - 35x - 49 = 0`
`x_3 = (35 + 7 sqrt(73))/24 ~~ "3,95";` `x_4 = (35 - 7 sqrt(73))/24 ~~ "-1,03"`
Ezek közül `x_1 in D` és `x_2 in D`, vagyis megoldásai az eredeti egyenletnek. Viszont `x_3 notin D` és `x_4 notin D`, vagyis ezek nem megoldások.
Jó kis feladat volt! Határozottan nem középiskolai, max emelt matekon lehet ilyen, de azért érdekes volt!
Határozottan nem középiskolai, max emelt matekon lehet ilyen, de azért érdekes volt!
`x^2-1 > 0`
`x^2 > 1 " /" sqrt`
`abs x > 1 => x in (-oo, -1) uu (1, oo)`
Illetve majd amikor lejjebb egy oldalra rendezem a gyökös kifejezést, abból láthatjuk, hogy mi marad az egyenlet másik oldalán, ami nem lehet negatív. Vagyis
`(12x)/(35-12x) >= 0`
Egy tört akkor nagyobb, mint 0, ha a számlálója és nevezője vagy nagyobb, vagy kisebb, mint 0. Nulla pedig akkor lehet, ha a számláló nulla, de a nevező nem nulla. Tehát:
`I.`
`{(12x >= 0, => x >= 0), (35-12x > 0, => x < 35/12):}`
`=> 0 <= x < 35/12 => x in [0, 35/12)`
`II.`
`{(12x <= 0, => x <= 0), (35-12x < 0, => x > 35/12):}`
`=> 35/12 < x <= 0 => x in O/`
Ezeket összegezve pedig azt kapjuk, hogy az értelmezési tartomány a következő:
`D = (1, 35/12) = (1; "2,91"dot 6)`
(Ezzel zárom majd ki a megoldások felét később!)
Most, hogy ez megvolt lássunk neki a feladatnak!
`(x)/sqrt(x^2-1) = 35/12-x` `" /" *12 sqrt(x^2-1)`
`12x = (35-12x)*sqrt(x^2-1)` `" /" :(35-12x)`
`(12x)/(35-12x) = sqrt(x^2-1)` `" /" ()^2`
`((12x)/(35-12x))^2 = x^2-1`
`(144x^2)/(35-12x)^2 = x^2-1` `" /" *(35-12x)^2`
`144x^2 = (x^2-1)(35-12x)^2`
`144x^2 = (x^2-1)(1225-840x+144x^2)`
`144x^2 = 1225x^2-840x^3+144x^4 - 1225+840x-144x^2`
`144x^4 - 840x^3 + 937x^2 + 840x - 1225 = 0`
Már eddig eljutni is elég szopás volt... Ami most jön csak még inkább az lesz! Tudjuk, hogy `144x^4=(12x^2)^2`, illetve hogy `1225 = 35^2`, de mivel 35 az `5*7`, ezért `35^2 = (5*7)^2 = 5^2*7^2 = 25*49`. Tehát valami ilyenre jó lenne szétbontani a fentit:
`(12x^2 + Ax + 25)*(12x^2 + Bx - 49)`
`144x^4 + 12Bx^3 - 12*49x^2 + 12Ax^3 + ABx^2 - 49Ax + 12*25x^2 + 25Bx - 1225`
`144x^4 + (12B+12A)x^3 + (-12*49+AB+12*25)x^2 + (-49A+25B)x - 1225`
Ezt a mi egyenletünkkel összevetve a következőt kapjuk:
`{("I.", 12A+12B = -840),("II.", AB+12(25-49) = 937),("III.", 25B-49A = 840):}`
A II.-on dolgozhatunk egy kicsit:
`AB-12*24 = 937`
`AB = 1225`
Illetve adja magát, hogy `-"III." = "I."`, tehát:
`12A+12B = 49A - 25B` `" /" -12A+25B`
`37A = 37B`
`A = B`
Ezt visszahelyettesítve az elsőbe megkapjuk, hogy
`A = B = -35`
Vagyis a szorzatunk nem más, mint:
`(12x^2 - 35x + 25)*(12x^2 - 35x - 49) = 0`
Innentől pedig már jelentősen könnyebb a dolgunk:
`I.`
`12x^2 - 35x + 25 = 0`
`x_1 = 5/4 = "1,25";` `x_2 = 5/3 = "1,6"dot 6`
`II.`
`12x^2 - 35x - 49 = 0`
`x_3 = (35 + 7 sqrt(73))/24 ~~ "3,95";` `x_4 = (35 - 7 sqrt(73))/24 ~~ "-1,03"`
Ezek közül `x_1 in D` és `x_2 in D`, vagyis megoldásai az eredeti egyenletnek. Viszont `x_3 notin D` és `x_4 notin D`, vagyis ezek nem megoldások.
Jó kis feladat volt!
 Határozottan nem középiskolai, max emelt matekon lehet ilyen, de azért érdekes volt!
Határozottan nem középiskolai, max emelt matekon lehet ilyen, de azért érdekes volt!
Módosítva: 3 éve
3
-
zalavaribotond: Ez a megoldás is tetszett, jól néz ki! 3 éve 1
-
Epyxoid: Köszi!
 3 éve
0
3 éve
0
 kazah
megoldása
kazah
megoldása
Először közelítsünk, számolni úgyse érdemes.
Egy szám (ami majd a megoldásunk lesz) és ami mellette van, az összege `35/12` = `2.91dot(6)` (legyen kb 3, úgy lazább )
)
A kezdeti feltétel alapján a szám 1-nél nagyobb és ha -1-nél kisebb lenne, akkor az összeg nem jön ki `approx` 3-ra. Tehát marad az, hogy pozitív és 1-nél nagyobb, de 3-nál kisebb. Sőt, ha kivonjuk azt a gyökös rettenetet, akkor azt is belátjuk, hogy 2-nél kisebb.
Ezzel nagyon leszűkült a kör, 1 és 2 közötti számot (számokat) keresünk. Mivel az egyenlet másodfokú tagot tartalmaz, kettőnél több gyököt nem érdemes keresni.
Hogyan tudnánk felbontani az összeget úgy, hogy kezelhető legyen?
`(a+b)/12=35/12`, ahol a és b is 13 és 23 között van (szűkül a kör)
a+b = 35
`a/12+a/root()(a^2-12^2) = 35/12`
A pitagorasz számhármasokat ha nem is mindet, de a 3-4-5-öt mindenki ismeri.
Így aztán olyat keresünk, aminek köze van a 12-höz, ez pedig (ha a fenti hármast szorozzuk 3-mal vagy 4-gyel), akkor szintén ilyen hármast kapunk.
I. 9-12-15 esetén
a = 15; b = 20
A bal oldali összeg az első esetben:
`15/12+20/12`
Ellenőrzés:
`15/12+(15/12)/(root()((15/12)^2-1)` = `15/12+15/root()(9^2)` = `15/12+5/3` = `(15+20)/12` = `35/12`
II. 12-16-20 esetén
a = 20; b = 15
`20/12+(20/12)/(root()((20/12)^2-1)` = `20/12+20/16` = `20/12+5/4` = `(20+15)/12` = `35/12`
Meg is van a két megoldásunk leellenőrizve, `20/12` és `15/12`
De elég nagy suttyóság ilyen feladatot adni, és ez csak egy közelítéses módszer.
Egy szám (ami majd a megoldásunk lesz) és ami mellette van, az összege `35/12` = `2.91dot(6)` (legyen kb 3, úgy lazább
 )
)A kezdeti feltétel alapján a szám 1-nél nagyobb és ha -1-nél kisebb lenne, akkor az összeg nem jön ki `approx` 3-ra. Tehát marad az, hogy pozitív és 1-nél nagyobb, de 3-nál kisebb. Sőt, ha kivonjuk azt a gyökös rettenetet, akkor azt is belátjuk, hogy 2-nél kisebb.
Ezzel nagyon leszűkült a kör, 1 és 2 közötti számot (számokat) keresünk. Mivel az egyenlet másodfokú tagot tartalmaz, kettőnél több gyököt nem érdemes keresni.
Hogyan tudnánk felbontani az összeget úgy, hogy kezelhető legyen?
`(a+b)/12=35/12`, ahol a és b is 13 és 23 között van (szűkül a kör)
a+b = 35
`a/12+a/root()(a^2-12^2) = 35/12`
A pitagorasz számhármasokat ha nem is mindet, de a 3-4-5-öt mindenki ismeri.
Így aztán olyat keresünk, aminek köze van a 12-höz, ez pedig (ha a fenti hármast szorozzuk 3-mal vagy 4-gyel), akkor szintén ilyen hármast kapunk.
I. 9-12-15 esetén
a = 15; b = 20
A bal oldali összeg az első esetben:
`15/12+20/12`
Ellenőrzés:
`15/12+(15/12)/(root()((15/12)^2-1)` = `15/12+15/root()(9^2)` = `15/12+5/3` = `(15+20)/12` = `35/12`
II. 12-16-20 esetén
a = 20; b = 15
`20/12+(20/12)/(root()((20/12)^2-1)` = `20/12+20/16` = `20/12+5/4` = `(20+15)/12` = `35/12`
Meg is van a két megoldásunk leellenőrizve, `20/12` és `15/12`
De elég nagy suttyóság ilyen feladatot adni, és ez csak egy közelítéses módszer.
1
-
Epyxoid: Hmm, sajnos nem értem, pedig érdekelne a gondolatmenet
 Honnan jött a `a/sqrt(a^2-12^2)` és a Potagoraszi számhármasok ötelete??
3 éve
0
Honnan jött a `a/sqrt(a^2-12^2)` és a Potagoraszi számhármasok ötelete??
3 éve
0
-
Epyxoid: Bocs, nem akartam két kérdőjelet tenni
 3 éve
0
3 éve
0
-
kazah: A racionális számhalmazon gondolkodtam. A gyökjel alá olyan kifejezés kerüljön, amiből gyökvonás után is racionális szám maradjon. Ezért kell a 12 körül forogni, ebből pedig van pár, még az 5-12-13 is eszembe jutott, csak nem vezetett jó eredményre
 3 éve
0
3 éve
0
-
kazah: Szerintem ez a feladat, ahogy láttam egy középiskolai feladatgyűjteményben van, nem a negyedfokúra van kiélezve; el lehet vele órákat játszani, de az hogy `35/12` az összeg, biztos nem légből kapott szám. De ez csak az én véleményem. 3 éve 0
-
kazah: A gyökös az már egy egyszerűsített alak, x helyére beírom `a/12`-t, akkor ott a nevezőben kiesnek a 12-k. 3 éve 0
-
yhrufcg5: Ez tetszik a legjobban, ötletes és nem kell annyit számolni, a negyedfokút amúgyis nehéznek gondolom. 3 éve 0