Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Abszolútértékes egyenlet
 yhrufcg5
kérdése
yhrufcg5
kérdése
391
Oldja meg a valós számok halmazán az alábbi egyenletet!
Jelenleg 1 felhasználó nézi ezt a kérdést.
abszolútérték, egyenlet
abszolútérték, egyenlet
0
Középiskola / Matematika
Válaszok
1 kazah
megoldása
kazah
megoldása
`|x^2-1|=-|x|+1`
Meg kell keresni azokat az intervallumokat, ahol a belső függvény előjelet vált.
Három eset lesz, a négyzetes függvény miatt kettő, a jobb oldal is hoz egyet. Ebből következik, hogy a három szám négy részre osztja a számhalmazt.
I. Ha x `le` -1 (É.T.)
`x^2-1=-(-x)+1`
`x^2-x-2=0`
`(x+1)(x-2)` = 0
szorzat akkor nulla, ha valamelyik tényezője nulla.
`x_1` = 2 `notin` É.T.
`x_2` = -1 `in` É.T.
II. Ha -1 `le` x `le` 0
`-x^2+1=-(-x)+1`
`x^2+x=0`
`x(x+1)=0`
szorzat akkor nulla, ha valamelyik tényezője nulla
`x_1=0` `in` É.T.
`x_2=-1` `in` É.T.
III. Ha 0 `le` x `le` 1:
`-x^2+1=-x+1`
`x^2-x=0`
Szorzat akkor nulla, ha valamelyik tényezője nulla.
`x(x-1)=0`
`x_1` = 0 `in` É.T.
`x_2` = 1 `in` É.T.
IV. Ha x `ge` 1
`x^2-1=-x+1`
`x^2+x-2=0`
`(x+2)(x-1)=0`
`x_1=-2` `notin` É.T.
`x_2` = 1 `in` É.T.
Megoldás: `x_1` = -1 ; `x_2` = 0 ; `x_3` = 1
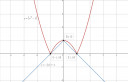
Ábra
Meg kell keresni azokat az intervallumokat, ahol a belső függvény előjelet vált.
Három eset lesz, a négyzetes függvény miatt kettő, a jobb oldal is hoz egyet. Ebből következik, hogy a három szám négy részre osztja a számhalmazt.
I. Ha x `le` -1 (É.T.)
`x^2-1=-(-x)+1`
`x^2-x-2=0`
`(x+1)(x-2)` = 0
szorzat akkor nulla, ha valamelyik tényezője nulla.
`x_1` = 2 `notin` É.T.
`x_2` = -1 `in` É.T.
II. Ha -1 `le` x `le` 0
`-x^2+1=-(-x)+1`
`x^2+x=0`
`x(x+1)=0`
szorzat akkor nulla, ha valamelyik tényezője nulla
`x_1=0` `in` É.T.
`x_2=-1` `in` É.T.
III. Ha 0 `le` x `le` 1:
`-x^2+1=-x+1`
`x^2-x=0`
Szorzat akkor nulla, ha valamelyik tényezője nulla.
`x(x-1)=0`
`x_1` = 0 `in` É.T.
`x_2` = 1 `in` É.T.
IV. Ha x `ge` 1
`x^2-1=-x+1`
`x^2+x-2=0`
`(x+2)(x-1)=0`
`x_1=-2` `notin` É.T.
`x_2` = 1 `in` É.T.
Megoldás: `x_1` = -1 ; `x_2` = 0 ; `x_3` = 1
Ábra
2
-
Epyxoid: Akkor jól emlékeztem, hogy így kell megoldani! Nice! Az ábra baromi jó lett!
 3 éve
0
3 éve
0
-
yhrufcg5: Köszönöm
 3 éve
0
3 éve
0