Körgyűrűcikk területe

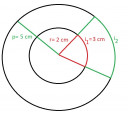
A rendelkezésre álló adatokból (se ábra, se az, hogy mi minek a sugara, hossza) erre tippelek:

`r/p=i_1/i_2`

`i_2=(i_1*p)/r` = `(3*5)/2` = 7,5 cm

És a lenti ábrát képzelem hozzá.

Ha pedig a területe is kell, akkor nem szükséges `i_2`-t kiszámolni; a nagy körcikk területéből kivonod a kis körcikk területét.

Kiszámolnám a középponti szöget, tehát azt, hogy a 2 cm sugarú kör 3 cm-es ívhéez mekkora középponti szög tartozik.

`(2*r*pi)/360*alpha` = `i_1`

`alpha` = `(i_1*360)/(2*r*pi)` = `(3*360)/(2*2*3.14)` = 85,94°.

A nagy körhöz tartozó körcikk területe:

`T_(kc)` = `(p^2*pi*alpha)/360` = `5^2*3.14*85.94/360` = 18,75 `cm^2`

A kis körhöz tartozó körcikk területe:

`t_(kc)` = `(r^2*pi*alpha)/360` = `(2^2*3.14*85.94)/360` = 3 `cm^2`

A keresett terület:

T = `T_(kc)-t_(kc)` = `18.75-3` = 15,75 `cm^2`

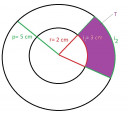
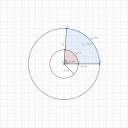
Csináltam ehhez is egy kis szemléltetést. Természetesen tükrözi kazah minden számítását. Csak egy kis vizuális segítségnek szánom. A meglévő megoldáshoz nem tesz hozzá.
Illetve akkor már pár képlet érdekességképpen! (megint csak kizárólag a hasonlóságok szemléltetése gyanánt)

1) Az ívhossz úgy aránylik a kör kerületéhez (teljes ívhosszhoz), mint a hozzátartozó szög a teljesszöghöz:
`i = K*alpha/360 = 2 pi r*alpha/360 = pi r*alpha/180` (`i:K = alpha:360° iff i/K = alpha/360`)

2) A körcikk területe úgy aránylik a kör területéhez (teljes körcikk), mint a hozzátartozó szög a teljesszöghöz:
`T_⌔ = T_○*alpha/360 = pi r^2*alpha/360` (`T_⌔:T_○ = alpha:360° iff T_⌔/T_○ = alpha/360`)

3) A körgyűrű cikk területe úgy aránylik a teljes körgyűrű területéhez, mint a hozzátartozó szög a teljesszöghöz:
`T_(⌔gy) = T_(○gy)*alpha/360 iff T_(⌔gy):T_(○gy) = alpha:360° iff T_(⌔gy)/T_(○gy) = alpha/360`
`[T_(○gy) = T_(○R)-T_(○r) = pi R^2 - pi r^2 = pi(R^2-r^2)]`
`[T_(⌔gy) = T_(⌔R)-T_(⌔r) = pi R^2*alpha/360 - pi r^2*alpha/360 = pi(R^2-r^2)*alpha/360]`