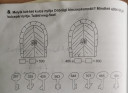
8) A bal oldali ajtóhoz olyan számpárokat keresünk, amiknek a különbsége nagyobb, mint 500. Mivel a kulcsok szépen növekvő sorrendben vannak, ezért szerintem érdemes a két végéről elindulni. Mondjuk vesszük az 1-es számú kulcsot (257), megnézzük mennyi hogy ha hozzáadunk 500-at és a másik oldalról elindulva megnézzük, hogy melyik kulcsok nagyobbak ennél a számnál. Tehát:
`257 + 500 = 757`
Azaz jó kulcspár a `(257; 991)`, mert `991>757` és a `(257;865)`, mert `865>757`.
Így az első, legkisebb számunkhoz találtunk 2 másik kulcsot, tehát máris van 2 kulcspárunk. Most mehetünk a balról második kulcsra, hátha ahhoz is találunk párokat...
`325 + 500 = 825 => (325; 991), (325; 865)`
Ehhez a kulcshoz is ugyanazokat a párokat találtuk, mert ezek között a legnagyobb a különbség. Már csak 1 kulcs hiányzik, ami biztos a következő kulcshoz tartozik majd. Nézzük:
`429 + 500 = 929 => (429; 991)`
Ezek tartoznak a baloldali ajtóhoz. Összegezve:
`(257; 991), (257;865), (325; 991), (325; 865), (429; 991)`

A jobboldali ajtó egy picit trükkösebb, de nem sokkal. Ugyanúgy a kisebb számok felől indulok el. Ez nem törvényszerű, csak egy önkényes döntés, de az sokat segít ha növekvő, vagy csökkenő sorrendben haladunk. Mivel én a kisebb számok felől indulok, ezért ez a kisebb szám lesz az ajtók alatt lévő egyenlőtlenségben. Vagyis ha behelyettesítünk ismeretleneket, akkor valahogy így nézne ki:
`400 < b-a < 600`

`[`Kis magyarázat: Mivel mi a kis számok felől megyünk, azért a szám amit választunk az az `a` lesz, mert az a kisebb, amit majd ki kell vonni a nagyobb számból, amit hozzá keresünk. A `b`-t pedig úgy tudjuk a legkönnyebben megtalálni, ha ezt az egyenlőtlenséget kicsit átalakítjuk:
`400+a < b < 600+a`
Ez pontosan ugyanazt jelenti, mint az előző, csak itt hozzáadtunk `a`-t minden oldalhoz. Az előző ajtónál is ezt csináltam, csak nem így magyaráztam, mert több, mint biztos, hogy ezt még nem tanultátok (vagy lehet igen, honnan tudhatnám), de könnyen belátható az előző ajtónál is, hogy ha `b-a`-nak többnek kell lennie 500-nál, akkor `b`-nek nagyobbnak kell lennie `a+500`-nál, ezért is ezt számoltam ki korábban. Itt pedig azt tesszük, hogy választunk egy számot, az lesz `a`, majd kiszámoljuk mennyi `a+400` és `a+600` és `b`-nek ezek között kell lennie, hogy a két szám nyissa az ajtót.`]`

Először megint nézzük 257-et:
`257+400 = 657; 257+600 = 857 => (257; 707)`
Tehát ha az `a = 257`, akkor `b` csakis 707 lehet! Nézzük tovább!
`a=325 => 325+400=725; 325+600=925 => b = 865 => (325; 865)`
`a=429 => 829<b<1029 => b={865; 991} => (429; 865), (429; 991)`
`a=563 => 563+400=963; 563+600=1163 => (563; 991)`
Az az a jobboldali ajtót a következő kulcspárok nyitják:
`(257; 707), (325; 865), (429; 865), (429; 991), (563; 991)`