Szia. Egy kis koordináta geometria, az egyik kedvencem!

a) Az `AB` oldal egyeneséről 2 dolgot tudunk: hogy rajta van az `A` pont és a `B` pont, ami pont elégséges ahhoz, hogy pontosan egy egyenest kapjunk általuk. Erre a következő képlet létezik:
`(y_2-y_1)(x-x_1) = (x_2-x_1)(y-y_1)`,
ahol az egyik pont `P_1(x_1; y_1)`, a másik pedig `P_2(x_2; y_2)`.

Ez az `A`, `B` pontok esetében a következőt adja:
`(4-0)(x-0) = (-2-0)(y-0)`
`4x = -2y`
`4x+2y = 0`
Ez az `AB` oldal egyenesének egyenlete. Többféleképpen is lehet rendezni, de ez jelenleg nem lényeges.

b) Itt most elgondolkodtam, hogy hogyan lehetne a legkönnyebben megmondani, hogy melyik szög a legnagyobb anélkül, hogy kiszámolnánk mindet, de nem igen jut eszembe semmi sem, úgyhogy szerintem kénytelenek vagyunk. (Megvan mi kellett volna! Kiszámoljuk az oldal hosszakat, mint ahogy a c) pontban tettem, - ami sokkalta egyszerűbb, mint a szögek kiszámolása - és egyszerűen a leghosszabb oldallal szemközti szög a legnagyobb... És láthatjuk is, hogy a `b` oldal a leghosszabb, tehát a `beta` szög lesz a legnagyobb és tényleg ez a helyzet. Csak most esett le!)

Szöget két vektor között tudunk számolni, így először elő kell állítanunk vektorokat. Ezt úgy tudjuk megtenni, hogy két pontot kivonunk egymásból. Pl.:
`vec (AB) = B - A = (x_B-x_A; y_B-y_A)`
Ekkor ez a vektor az `A` pontból a `B`-be mutat. Ennek a fordítottja is lehetséges. Két vektor szöge pedig a két vektor kiindulópontjából értelmezett, tehát a vektoroknak is a jó irányban kell állniuk, különben nem a jó szöget kapjuk.

Legyen mondjuk az `A` pontnál lévő szög `alpha`, a `B`-nél lévő `beta`, a `C`-nél pedig `gamma`. Ekkor az `alpha` szöghöz az `vec (AB)` és az `vec (AC)` vektorokra van szükségünk, a `beta`-hoz `vec (BA)`-ra és `vec (BC)`-re, `gamma`-hoz pedig `vec (CA)`-ra és `vec (CB)`-re. Láthatjuk, hogy előállnak így ellentétes irányú vektorok, mint például az `vec (AB)` és `vec (BA)`. Ezek között csak annyi a különbség, hogy az egyik a másik mínusza, de számít az irányuk a szögek kiszámításakor.

Ha van két vektorunk, mondjuk `a (a_x; a_y)` és `a (b_x; b_y)`, akkor a közrezárt szögük `alpha` a következőképpen adódik:
`cos alpha = (a * b)/(abs a * abs b) = (a_x b_x + a_y b_y)/(sqrt (a_x^2 + a_y^2) * sqrt (b_x^2 + b_y^2))`,
ahol `a * b` a skaláris szorzást jelöli, `abs a` pedig a vektor hosszát.

`vec (AB) (-2; 4), vec (AC) (4; 5) => cos alpha = (-2*4 + 4*5)/(sqrt ((-2)^2 + 4^2) * sqrt (4^2 + 5^2)) = 6/sqrt 205 => alpha = cos^-1 (6/sqrt 205) = 65,2°`
`vec (BA) (2; -4), vec (BC) (6; 1) => cos beta = (2*6 + (-4)*1)/(sqrt (2^2 + (-4)^2) * sqrt (6^2 + 1^2)) = 4/sqrt 185 => beta = cos^-1 (4/sqrt 185) = 72,9°`
Mivel tudjuk, hogy a háromszög belső szögeinek összege `180°`, így
`gamma = 180° - alpha - beta = 41,9° [ = cos^-1 (29/sqrt (37*41))]` (csak a teljesség végett (ebben van a legtöbb prím))

Így tehát a `/_\\` legnagyobb szöge `72,9°`!

c) Mivel már számoltunk oldal hosszakat és szögeket, így mondjuk a `T = (ab sin gamma)/2` megteszi a végtelen sok terület képlet közül.
Tehát ha az `a` oldal az `alpha` szöggel szemközti, a `b` a `beta`-val, a `c` a `gamma`-val, akkor
`a = abs vec(BC) = sqrt (6^2+1^2) = sqrt 37`
`b = abs vec(AC) = sqrt (4^2+5^2) = sqrt 41`
`c = abs vec(AB) = sqrt ((-2)^2+4^2) = sqrt 20`
Ekkor `T = (sqrt (37*41) sin 41,9°)/2 = 13` (kereken)

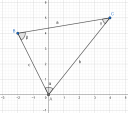
Egy kis extra szemléltetés. (Sajnos az eredeti válaszomhoz már nem tudtam csatolni.)