Úú, jó kis koordináta geometria! Lássuk!

Tudjuk, hogy ott, ahol egy egyenes érint egy kört, arra merőlegesen metsszük a kör középpontját, vagyis ha összekötjük azt a két pontot, ahol érinti az egyenes a kört, akkor félúton ezen az egyenesen rajta lesz a kör középpontja és ez az egyenes pont merőleges arra az egyenesre, amivel érintjük a kört.

Amit tehetünk az az, hogy először megnézzük mekkora az egyenes meredeksége, abból kiszámoljuk az erre merőleges meredekséget és ebből a meredekségből és a kör középpontjából felírunk egy egyenes egyenletet és ahol ez az egyenes metszi a kört, az lesz az a két pont, ami az egyenessel párhuzamos két érintőt adja.

Az egyenesünk:
4x - 2y = 7
Fejezzük ki belőle y-t!
2y = 4x - 7
y = 2x - 7/2
Ebből adódik, hogy a meredekség m = 2 (illetve az is, hogy ez az egyenes y0 = -7/2-nél metszi az y tengelyt, bár ez most nem lényeges)

Ebből a meredekségből úgy képzünk egy erre merőleges meredekséget, hogy vesszük a mínuszát és a reciprokát:
m⦜ = -1/m = -1/2

Most lássuk a körünket:
x2 + y2 = 25
Tudjuk, hogy (x - u)2 + (y - v)2 = r2, ahol (u; v) a kör középpontja, és r a kör sugara. Jelen esetben:
(u; v) = (0; 0) és r = 5

Tehát az az egyenes, ami az eredeti egyenesre merőleges és áthalad a kör középpontján:
C(0; 0), m⦜ = -1/2 ⇒
y - 0 = -1/2∙(x - 0)
y = -1/2x

Ezek után két olyan pontot keresünk, ami egyszerre kielégíti a kör egyenletét (rajta van a körön) és kielégíti az imént megkapott egyenes egyenletét is (rajta van az egyenesen), azaz a két egyenletet összekapcsoljuk egy egyenletrendszerré és megoldjuk!
(I) x2 + y2 = 25
(II) y = -1/2x
Egyből be is helyettesíthetjük y-t (II) a kör egyenletébe (I):
x2 + (-1/2x)2 = 25
x2 + 1/4x2 = 25
5/4x2 = 25
x2 = 25∙4/5 = 20
x1,2 = ±√ 20  = ±2√ 5 

Ezeket az értékeket visszahelyettesítve az egyenes egyenletébe (II) azt kapjuk, hogy:
y1,2 = ±√ 5 

Tehát a két pont:
P1(2√ 5 ; -√ 5 ), P2(-2√ 5 ; √ 5 )

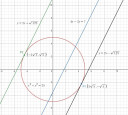
Tehát van egy körünk, aminek az egyenlete:

`x^2+y^2=25`

Továbbá olyan egyenest keresünk, amelynek a meredeksége 2 és egy közös pontjuk van.

`y=2x+b`

Az egyenes egyenletét behelyettesítjük a kör egyenletébe:

`x^2+(2x+b)^2=25`

`x^2+4x^2+4bx+b^2=25`

`5x^2+4bx+(b^2-25)=0`

Ha érintő, akkor egy közös pont van, vagyis a diszkrimináns nulla.

`(4b)^2-4*5*(b^2-25)=0` /:4

`4b^2-5b^2+125=0`

`b^2=125`

`b_1=root()(125)` = `5*root()(5)`

`b_2=-5*root()(5)`

A két egyenes egyenlete tehát:

`y=2x+5*root()(5)` és

`y=2x-5*root()(5)`

Ábra