Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Segítsetek
 kilbilevi
kérdése
kilbilevi
kérdése
514
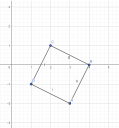
Az ABCD négyszög csúcsai A(3; -2), B(4; 0), C(2; 1), D(1; -1) pontok. Bizonyítsd be, hogy ABCD négyszög téglalap.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
3 bazsa990608
{ Közgazdász }
megoldása
bazsa990608
{ Közgazdász }
megoldása
Csatoltam képet és számítást.
Az olyan téglalapot, melynek minden oldala ugyanolyan hosszúságú négyzetnek nevezzük.
Tehát ez egy téglalap.
Az olyan téglalapot, melynek minden oldala ugyanolyan hosszúságú négyzetnek nevezzük.
Tehát ez egy téglalap.
Módosítva: 3 éve
1
- Még nem érkezett komment!
 kemenyb
{ Elismert }
válasza
kemenyb
{ Elismert }
válasza
Jó az első válasz, de ennek egyszerűbb megoldása a következő:
A téglalap átlói egyenlő hosszúak. Az átlók legyenek: e=AC, f=BD
e=sqrt((2-3)^2+(1-(-2))^2)=sqrt(1+9)=sqrt(10)
f=sqrt((1-4)^2+((-1)-0)^2)=sqrt(9+1)=sqrt(10)
Tehát ez egy téglalap.
A téglalap átlói egyenlő hosszúak. Az átlók legyenek: e=AC, f=BD
e=sqrt((2-3)^2+(1-(-2))^2)=sqrt(1+9)=sqrt(10)
f=sqrt((1-4)^2+((-1)-0)^2)=sqrt(9+1)=sqrt(10)
Tehát ez egy téglalap.
0
- Még nem érkezett komment!
 kazah
válasza
kazah
válasza
Alakul, srácok, de még mindig nem az igazi 
Mindig azt kell végiggondolni, hogy mitől lesz egy téglalap téglalap.
Bazsával már megbeszéltük, lehet, hogy a kérdező se jön már vissza, de az oldalak egyenlősége kevés (rombusz is lehet). Az ábrázolás jó, de ha ránézek egy négyzetnek látszó síkidomra, az még nem biztos, hogy négyzet.
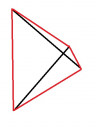
A másodikra: egyenlők az átlók? akkor húrtrapéz is lehet, de egy olyan négyszög is, melynek az átlói egyenlő hosszúak (ábra).
Eddig itt tartunk.
Ha nagyon akarjuk bizonyítani, hogy gondoljuk végig, hogy mi a feltétele a téglalapnak. Párhuzamos oldalpárok, szomszédos oldalak merőlegesek. A koordinátageometriában könnyű ezeket bizonygatni.
`m_1` = `(y_B-y_A)/(x_B-x_A)` = `(0-(-2))/(4-3)` = `2`
`m_2` = `(y_C-y_B)/(x_C-x_B)` = `(1-0)/(2-4)` = `-1/2`
`m_3` = `(y_D-y_C)/(x_D-x_C)` = `(-1-1)/(1-2)` = `-2/(-1)` = `2`
`m_4` = `(y_A-y_D)/(x_A-x_D)` = `(-2-(-1))/(3-1)` = `(-1)/2` = `-1/2`
`m_1=m_3` és `m_2=m_4`, valamint `m_1=-1/m_2`; így mindent bizonyítottunk a téglalapra vonatkozóan, szóval az se lényeg, hogy négyzet.
A másodiknál: A téglalap átlói felezik egymást, azt is kéne bizonyítani, lehet, csak kicsit hosszadalmasabb.

Mindig azt kell végiggondolni, hogy mitől lesz egy téglalap téglalap.
Bazsával már megbeszéltük, lehet, hogy a kérdező se jön már vissza, de az oldalak egyenlősége kevés (rombusz is lehet). Az ábrázolás jó, de ha ránézek egy négyzetnek látszó síkidomra, az még nem biztos, hogy négyzet.
A másodikra: egyenlők az átlók? akkor húrtrapéz is lehet, de egy olyan négyszög is, melynek az átlói egyenlő hosszúak (ábra).
Eddig itt tartunk.
Ha nagyon akarjuk bizonyítani, hogy gondoljuk végig, hogy mi a feltétele a téglalapnak. Párhuzamos oldalpárok, szomszédos oldalak merőlegesek. A koordinátageometriában könnyű ezeket bizonygatni.
`m_1` = `(y_B-y_A)/(x_B-x_A)` = `(0-(-2))/(4-3)` = `2`
`m_2` = `(y_C-y_B)/(x_C-x_B)` = `(1-0)/(2-4)` = `-1/2`
`m_3` = `(y_D-y_C)/(x_D-x_C)` = `(-1-1)/(1-2)` = `-2/(-1)` = `2`
`m_4` = `(y_A-y_D)/(x_A-x_D)` = `(-2-(-1))/(3-1)` = `(-1)/2` = `-1/2`
`m_1=m_3` és `m_2=m_4`, valamint `m_1=-1/m_2`; így mindent bizonyítottunk a téglalapra vonatkozóan, szóval az se lényeg, hogy négyzet.
A másodiknál: A téglalap átlói felezik egymást, azt is kéne bizonyítani, lehet, csak kicsit hosszadalmasabb.
2
-
kemenyb: Jogos, benéztem az átlókat. 3 éve 0
-
kilbilevi: Ha én rám gondoltak, de igen, visszajövök. Igazából nem nekem kellett a megoldás.. ha az én feladatom lett volna, akkor megoldottam volna egyedül. 3 éve 0