1,

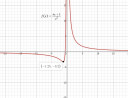
`f(x)=(8x+5)/x^2`

`x ne 0` `rightarrow` A 0 az egyik kritikus hely. Továbbá érdemes megvizsgálni `pm oo`-nél is.

`lim_(x rightarrow oo) (8x+5)/x^2` = `ubrace(lim_(x rightarrow oo) 8/x)_(0^+)` + `ubrace(lim_(x rightarrow oo) 5/x^2)_(0^+)` = `0^+`

`lim_(x rightarrow -oo) (8x+5)/x^2` = `ubrace(lim_(x rightarrow -oo) 8/x)_(0^-)` + `ubrace(lim_(x rightarrow -oo) 5/x^2)_(0^-)` = `0^-`

`lim_(x rightarrow 0^+) (8x+5)/x^2` = `ubrace(lim_(x rightarrow 0^+) 8/x)_(+oo)` + `ubrace(lim_(x rightarrow 0^+) 5/x^2)_(+oo)` = `+oo`

`lim_(x rightarrow 0^-) (8x+5)/x^2` = `ubrace(lim_(x rightarrow 0^-) 8/x)_(-oo)` + `ubrace(lim_(x rightarrow 0^-) 5/x^2)_(+oo)` = `+oo`

A helyi szélsőértékeket az első deriváltból tudhatjuk meg:

`f'(x)` = `(d(f(x)))/(dx)` = `d/dx((8x+5)/x^2)` = `d/dx(8/x)+d/dx(5/x^2)` = `-8/x^2+(-10/x^3)`

`-8/x^2+(-10/x^3)=0`

`-1/x^2*(8+10/x)=0`

`x ne 0`

`8+10/x=0` `rightarrow` `x=-5/4`

y = `(8*(-5/4)+5)/(-5/4)^2` = `(-5)/(25/16)` = `-16/5`

A függvénynek helyi szélsőértéke van a `(-5/4;-16/5)` pontban.


2,

a, Kritikus pontok: Zérushely, szélsőérték, inflexiós pont.

Zérushely: f(x) = 0

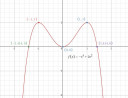
`-x^4+2x^2=0`

`x^2*(x^2-2)=0`

Szorzat akkor nulla, ha valamelyik tényezője nulla.

`x^2=0` `rightarrow` `x_1=0`

`x^2-2=0` `rightarrow` `x_2=root()(2)` ; `x_3` = `-root()(2)`

szélsőértékek: első derivált nulla

`f'(x)` = `d/dx(-x^4+2x^2)` = `-4x^3+4x`

`-4x^3+4x=0`

`4x*(1-x^2)=0`

`x_1=0` `rightarrow` `f(x1)=0`

`x_2=1` `rightarrow` `f(x2)=1`

`x_3=-1` `rightarrow` `f(x3)=1`


Inflexiós pont: második derivált nulla

`f''(x)` = `d/dx(-4x^3+4x)` = `-12x^2+4`

`12x^2=4` `rightarrow` `x_(i1)` = `-root()(1/3)`

`x_(i2)` = `root()(1/3)`


Monotonitás:

`]-oo;-1[` szigorúan monoton növekvő

`]-1;0[` szigorúan monoton csökkenő

`]0;1[` szigorúan monoton növekvő

`]1;oo[` szigorúan monoton csökkenő