Csatoltam képet.

16,

Kicsit átrendezzük a kör egyenletét:

`x^2-6x+y^2+8y-56=0`

`(x-3)^2-9+(y+4)^2-16-56=0`

`(x-3)^2+(y+4)^2=81` `(=9^2)`

Egyenes: x=8,4

Behelyettesítünk a kör egyenletébe:

`(8.4-3)^2+(y+4)^2=81`

`(y+4)^2=51.84`

`y_1+4=7.2` `rightarrow` `y_1` = 3,2

`y_2+4=-7.2` `rightarrow` `y_2` = -11,2

A közös pontok: E(8,4;3,2) és F(8,4;-11,2).

b,

Pont távolsága az egyenestől.

x=8,4 O(3;-4)

A függőleges egyenesen megkeressük azt a pontot, aminek a távolságát kell keresni a kör középpontjától.

P(8,4;-4)

A távolság pedig az x koordináták különbsége lesz (abszolútértéke).

`d_(OP)` = `|8.4-3|` = 5,4

c,

A c rész nem koordinátageometriai feladat, lehetett volna külön sorszámot adni neki

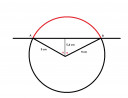
Ábra

`cosalpha=5.4/9` = 0,6

`alpha` = 53,13°.

A nagyobbik körívhez tartozó középponti szög:

`360-2*alpha` = `360-2*53.13` = 253,74°.

`l=2*r*pi*253.74/360` = `2*9*3.14*253.74/360` = 39,9 cm.