1,

m = `(y_B-y_A)/(x_B-x_A)` = `(-5-3)/(1-(-5))` = `-8/6` = `-4/3`

3 = `-5*(-4/3)+b`

b = `-11/3`

y = `-4/3*x-11/3` vagy 4x+3y+11=0

Ábra

2,

`x^2+y^2+2x-4y-20=0`

`(x^2+2x+1)-1+(y^2-4y+4)-4-20=0`

`(x+1)^2+(y-2)^2=5^2`

O(-1;2) ; r = 5

b,

e: y = 4-3x

k: `(x+1)^2+(4-3x-2)^2=25`

`x^2+2x+1+9x^2-12x+4=25`

`10x^2-10x-20=0`

`x^2-x-2=0`

szorzattá alakítás:

`(x-2)(x+1)=0`

`x_1` = 2 `rightarrow` `y_1` = `4-3*2` = -2

`x_2` = -1 `rightarrow` `y_2` = `4+3*1` = 7

A közös pontok:

A(2;-2) és B(-1;7)

Ábra

3,

`x^2+y^2-4x+2y-32=0`

`(x^2-4x+4)-4+(y^2+2y+1)-1-32=0`

`(x-2)^2+(y+1)^2=37`

A pontba húzott sugár egyenlete:

O(2;-1) ; P(3;-7)

m = `(y_B-y_A)/(x_B-x_A)` = `(-7-(-1))/(3-2)` = -6

`m_e` =`-1/m` = `1/6`

A keresett egyenes meredeksége `1/6`.

`-7=1/6*3+b`

b = `-15/2`

A keresett egyenes egyenlete:

`y=1/6*x-15/2` vagy x-6y-39=0

4,

Az egyenes meredeksége:

m = `-4/3`

Az erre merőleges egyenes meredeksége: `m_1` = `3/4`

Az adott pontot felhasználva:

`-1=3/4*1+b`

b = `-7/4`

Az egyenes egyenlete:

y = `3/4*x+7/4` vagy 4y-3x=7

A két egyenes metszéspontja:

I. 4y-3x=7 (*3)

II. 4x+3y=24 (*4)

I. 12y-9x=-21

II. 16x+12y=96

II. - I.:

25x = 75

x = 3

I.: `4*y-3*3=7` `rightarrow` y = `(7+9)/4` = 4

A metszéspont koordinátái:

O(3;4)

`d_(AO)` = `root()((x_A-x_o)^2+(y_A-y_O)^2)` = `root()((-1-3)^2+(1-4)^2)` = `root()(4^2+3^2)` = 5

A tükörkép koordinátái:

`x_B` = `x_O+|x_A-x_O|` = `3+|-1-3|` = 7

`y_B` = `y_O+|y_A-y_O|` = `4+|1-4|` = 7

B(7;7)

5,

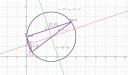
Keressünk meg két oldalfelező merőleges egyenletét, annak a metszéspontja lesz a kör középpontja; a kör sugara pedig a középpont és az egyik csúcs távolsága.

A(1;1) és B(0;4)

Az AB egyenes meredeksége:

`m_(AB)` = `(y_B-y_A)/(x_B-x_A)` = `(4-1)/(0-1)` = -3

Az AB oldalfelező pontja:

`x_D` = `(x_A+x_B)/2` = `1/2`

`y_D` = `(y_A+y_B)/2` = `5/2`

D(`1/2;5/2`)

Az AB oldalfelező merőleges kiszámítása:

`5/2=1/3*1/2+b_1` `rightarrow` `b_1=7/3`

Első egyenlet: `y=1/3*x+7/3` vagy `color(red)(3y-x=7)`

A BC egyenes meredeksége:

`m_(BC)` = `(y_C-y_B)/(x_C-x_B)` = `(7-4)/(9-0)` = `1/3`

A BC oldalfelező pontja:

`x_E` = `(x_B+x_C)/2` = `9/2`

`y_E` = `(y_B+y_C)/2` = `11/2`

E(`9/2;11/2`)

A BC oldalfelező merőleges kiszámítása:

`11/2=-3*9/2+b_2` `rightarrow` `b_2=19`

A második egyenlet: `color(red)(y=-3x+19)` vagy `color(red)(y+3x=8)`

I. 3y-x=7

II. y = -3x+19

I. 3(-3x+19)-x=7

10x=50

x = 5

I. 3y-5=7

y = 4

A kör középpontja: O(5;4)

A kör sugara: (a legegyszerűbb a B ponttól lesz vizsgálni)

`d_(BO)` = `root()((x_B-x_O)^2+(y_B-y_O)^2)` = |0-5| = 5

A kör egyenlete tehát:

`(x-5)^2+(y-4)^2=5^2`.