Matek feladatok

1, Ábra

2, A konvex sokszög belső szögeinek összege `(n-2)*180`. A konvex sokszög átlóinak száma `(n*(n-3))/2`.

`(n-2)*180` = 2520

n-2 = `2520/180` = 14

n = 14+2 = 16

`(n*(n-3))/2` = `(16*(16-3))/2` = 104 átlója van a konvex 16-szögnek.

3,

`i` = `(2*r*pi)*115/360` = `(2*5*3.14)*115/360` `approx` 10,04 cm

4,

Ha a kör sugarát háromszorosára növeljük, akkor a területe `3^2` = 9-szeresére nő.

5,

a,

`3*65000` = 195.000 cm = 1950 m = 1,95 km

Legyen négyzet alakú a liget a könnyebb áttekinthetőség és számolás szempontjából.

Ekkor a liget oldala `root()(9)` = 3 km hosszú, ami 3000 m = 300.000 cm.

A térképen ez `300000/65000` = 4,615 cm

A 4,615 cm oldalú négyzet területe T = `a^2` = `4.615^2` = 21,3 `cm^2`

6,

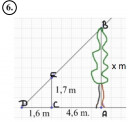
Keressük a hasonló háromszögeket, ugyanis azokban a megfelelő oldalak aránya egyenlő.

DCE háromszög hasonló az ABD háromszöghöz.

`(CD)/(CE)=(CD+AC)/(AB)`

`1.6/1.7=(1.6+4.6)/x`

x = `((1.6+4.6)*1.7)/1.6` = 6,5875 m magas a fa.

7,

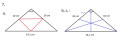
A háromszög átfogója c = `10*root()(2)` cm `approx` 14,1 cm.

a, A középvonalak hossza feleannyi, mint a háromszög oldalainak hossza. 5, 5 és 7,05 cm.

b, Az átfogóhoz tartozó súlyvonal egyben a háromszög átfogóhoz tartozó magassága is. Ezt a területből tudjuk egyszerűen számolni:

T = `a^2/2=(c*m_c)/2`

`s_c` = `m_c` = `a^2/c` = `10^2/(10*root()(2)` = `5*root()(2)` `approx` 7,07 cm.

c, A befogó(k)hoz tartozó súlyvonal(ak) hosszát Pitagorasz-tétellel tudjuk számolni, keressük a megfelelő derékszögű háromszöget:

`s_a` = `root()(10^2-5^2)` = `root()(75)` `approx` 8,66 cm

d,

A súlypont a súlyvonalakat 2:1 arányban osztja (a csúcsoktól van a távolabbi rész, ahogy az ábrán is látod). A súlyvonalakat tehát szorzod `2/3`-dal és meg is vannak a válaszok:

`d_A` = `d_B` = `2/3*root()(75)` `approx` 5,77 cm

`d_C` = `2/3*(5*root()(2))` `approx` 4,71 cm.