I./ 1.

Ha a negyedkör területe 36,1 `cm^2`, akkor a kör területe `36.1*4` = 144,4 `cm^2`

T = `r^2*pi` `rightarrow` r = `root()(T/pi)` = `root()(144.4/3.14)` = 6,78 cm

A kör kerülete az 360°-os középponti szöghöz tartozik.

K = `2*r*pi`

117°-os középponti szöghöz:

`l` = `K*117/360` = `(2*r*pi)*117/360` = `(2*6.78*3.14)*117/360` = 13,84 cm.


II./1.

A terület ugyanúgy, mint fent, így a sugár is annyi.

A kör kerülete:

K = `2*r*pi` = `2*6.78*3.14` = 42,96 cm. Ekkora körív tartozik 360°-os középponti szöghöz.

7 cm-es körívhez tartozik `7/42.96*360` = 58,65°-os központi szög.


3,

a,

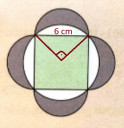
Először szükségünk van a (fehér) kör sugarára. Az ábrán berajzolt egyenlőszárú derékszögű háromszögből kiszámolhatjuk; ismerjük az átfogóját, a befogó hossza:

r = `a/root()(2)` = `6/root()(2)` = `3*root()(2)` cm

A 90°-os körcikk területe:

`T_(kc)` = `(r^2*pi)/4` = `4.5*pi` `cm^2`

A fehér körszelet területét megkapjuk, ha a körcikk területéből kivonjuk a fentebb használt derékszögű háromszög területét:

`T_(ksz)` = `T_(kc)-T_3` = `4.5*pi-r^2/2` = `4.5*pi-9` `cm^2`

A kérdéses terület tehát ennek a négyszerese (mivelhogy 4 van belőle):

`T_1` = `4*T_(ksz)` = `18*pi-36` `approx` 20,55 `cm^2`

b,

A négyzet oldalára rajzolt félkörök területe:

`T_(fk)` = `(a^2*pi)/(2*4)` = `(6^2*pi)/8` = `4.5*pi` `cm^2`

Ebből kivonjuk a körszelet területét:

`T_(sz)` = `T_(fk)-T_(ksz)` = `4.5*pi-(4.5*pi-9)` = `9` `cm^2`

Ebből is négy van, a kérdéses terület:

`T_2` = `4*T_(sz)` = `4*9` = 36 `cm^2`

c,

A négyzet területe:

`T_n` = `a^2` = `6^2` = 36 `cm^2`. Igaz.