Így érthető a válasz? (Érdemes a többivel is foglalkozni?)
A kommentben kiderült, hogy talán az algebrai megoldásra lenne szükséged. Azt is megcsináltam. ( hátha annak annak is tetszik, aki a geometriai megoldást "lepontozta"?! )
Itt nézheted meg a teljes megoldást:
https://www.geogebra.org/m/Vv7BU9bn

A 3) a legkönnyebb, azt talán megérted:

Kell hozzá tudni egy ilyen dolgot:
`sqrt(valami^2) = |valami|`
Szóval ha valamit négyzetre is emelünk és utána gyököt vonunk belőle, nem ugyanazt a valamit kapjuk meg, hanem annak az abszolút értékét.
Pl. `sqrt((-2)^2)=sqrt((-2)·(-2))=sqrt(4)=2` ami ugyanaz, mint `|-2|`

Most ez lesz:
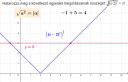
`sqrt((x-2)^2)=3`
`|x-2|=3`

Ha látsz valahol egy abszolút érték jelet, akkor meg kell nézni, mikor 0 az, ami belül van. Azért kell, mert annál kisebb illetve nagyobb x-eknél máshogy viselkedik az abszolút érték.

Szóval mikor nulla x-2? x=2-nél.

a) x < 2
Ilyenkor x-2 < 0. Negatívnak kell az abszolút értékét venni. Az ugyanaz, mintha megszoroznánk -1-gyel, tehát az |x-2|=3-ből ez lesz:
`-(x-2) =3`
`-x+2=3`
`x=-1`

b) x ≥ 2
Ilyenkor x-2 ≥ 0. Pozitívnak kell az abszolút értékét venni. Az pedig egyszerűen önmaga, vagyis az |x-2|=3-ből ez lesz:
`(x-2) =3`
`x=5`

Tehát a két megoldás -1 és 5.
Az összeg 4, ahogy a zárójelben is van.

Én maradok a grafikus megoldásoknál:
(A másodiknál lemaradt az eredmény: 6*(-2/3)+1=-3 )

Az 1) a második legkönnyebb.

`|x|-2|x+1|+3|x+2|=0`

Most 3 abszolút érték is van, mindháromnál meg kell nézni, mikor 0 a belseje:
• x=0
• x+1=0 → x=-1
• x+2=0 → x=-2
Sorbarakva ezek tehát az érdekes x értékek: -2, -1, 0

A 3) feladatnál csak egy érdekes érték volt, most 3. Ott azt kellett nézni, hogy mi történik az érdekes értéknél kisebb és nagyobb x-eknél, itt pedig a számegyenes megfelelő intervallumain, ahogy mutatom:

a) x < -2:
Nézzük, ebben az intervallumban melyik milyen előjelű:
• x: negatív, ezért |x|-ből -(x) lesz
• x+1: negatív, ezért |x+1|-ből -(x+1) lesz
• x+2: negatív, ezért |x+2|-ből -(x+2) lesz
Ez lett:
`-(x)-2(-(x+1))+3(-(x+2))=0`
`-x+2(x+1)-3(x+2)=0`
`-x+2x+2-3x-6=0`
`-2x-4=0`
`-4=2x`
`x=-2`
Ez az a) rész olyan kell legyen, hogy x < -2 (nézd meg fent az a)-nál), de a -2 nem kisebb -2-nél, tehát ez nem megoldás.

b) -2 ≤ x < -1:
Nézzük, ebben az intervallumban melyik milyen előjelű:
• x: negatív, ezért |x|-ből -(x) lesz
• x+1: negatív, ezért |x+1|-ből -(x+1) lesz
• x+2: pozitív, ezért |x+2|-ből ugyanaz, (x+2) lesz
Ez lett:
`-(x)-2(-(x+1))+3(x+2)=0`
`-x+2(x+1)+3(x+2)=0`
`-x+2x+2+3x+6=0`
`-x+2x+2+3x+6=0`
`4x+8=0`
`x=-2`
Itt a b) résznél az az x-re a feltétel, hogy -2 ≤ x < -1, ezért ez jó megoldás.

c) -1 ≤ x < 0:
Nézzük, ebben az intervallumban melyik milyen előjelű:
• x: negatív, ezért |x|-ből -(x) lesz
• x+1: pozitív, ezért |x+1|-ből ugyanaz, (x+1) lesz
• x+2: pozitív, ezért |x+2|-ből ugyanaz, (x+2) lesz
Ez lett:
`-(x)-2(x+1)+3(x+2)=0`
`-x-2x-2+3x+6=0`
Az x-ek kiesnek!
`4=0`
Ez pedig lehetetlen, tehát ezen az intervallumon nincs megoldás.

d) 0 ≤ x:
Nézzük, ebben az intervallumban melyik milyen előjelű:
• x: pozitív, ezért |x|-ből ugyanaz, (x) lesz
• x+1: pozitív, ezért |x+1|-ből ugyanaz, (x+1) lesz
• x+2: pozitív, ezért |x+2|-ből ugyanaz, (x+2) lesz
Ez lett:
`(x)-2(x+1)+3(x+2)=0`
`x-2x-2+3x+6=0`
`2x+4=0`
`x=-2`
Itt a d) résznél az az x-re a feltétel, hogy 0 ≤ x, ezért ez nem megoldás ezen az intervallumon.

Tehát az egyetlen megoldás a b) intervallumnál volt, x=-2

A 2) a legnehezebb.

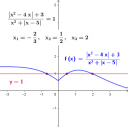
`(|x^2-4x|+3)/(x^2+|x-5|)=1`
Először egy kikötés kell: a nevező nem lehet 0
Mivel a nevezőben x² is pozitív meg |x-5| is pozitív, mindkettőnek 0-nak kellene lennie, hogy az összegük 0 legyen. x² akkor 0, ha x=0, de ekkor |x-5|=5, tehát nincs olyan x, aminél a nevező 0 lenne. Nincs kikötés.

Szorozzunk át a nevezővel:
`|x^2-4x|+3=x^2+|x-5|`

Most két abszolút érték van, azokat kell megnézni, hogy mikor lesz 0 a belsejük:
• `x-5 = 0`
→ `x_1=5`
• `x^2-4x=0`
→ `x(x-4)=0`
→ `x_2=0; x_3=4`

Tehát három helyen is lesz valahol nulla. Sorbarakva: 0, 4, 5
Ehhez négy intervallum tartozik:

a) x < 0:
• `x-5` negatív: ezért |x-5|-ből ez lesz: `-(x-5)`
• `x^2-4x` pozitív: (úgy jön ki legegyszerűbben, hogy pozitív, hogy mondjuk x=-1-et helyettesítünk be. Bármi más is lehetne, ami 0-nál kisebb, a -1 a legegyszerűbb.)
Szóval pozitív, ezért önmaga lesz: `(x^2-4x)`
`(x^2-4x)+3=x^2+(-(x-5))`
`x^2-4x+3=x^2-x+5`
`-3x=2`
`x=-2/3`
Ez megfelel az intervallumnak, tehát jó megoldás.

b) 0 ≤ x < 4:
• `x-5` negatív: ezért |x-5|-ből ez lesz: `-(x-5)`
• `x^2-4x` negatív: (úgy jön ki legegyszerűbben, hogy negatív, hogy mondjuk x=1-et helyettesítünk be. Elvileg x=0 is az intervallumban van, de arra 0 jön ki, nem tudjuk róla az előjelet, mással kell megnézni.)
Szóval negatív, ezért ez lesz: `-(x^2-4x)`
`-(x^2-4x)+3=x^2+(-(x-5))`
`-x^2+4x+3=x^2-x+5`
`5x=2x^2+2`
`2x^2-5x+2=0`
Megoldóképletből:
`{::}_2x_1=(5+-sqrt(5^2-4·2·2))/(2·2)=(5+-sqrt(9))/(4)=(5+-3)/4`
`x_1=2`
`x_2=1/2`

Ezek mindkettő benne az intervallumban, jók.

b) 4 ≤ x < 5:
• `x-5` negatív: ezért |x-5|-ből ez lesz: `-(x-5)`
• `x^2-4x` pozitív: (próbáld x=4,5-lel), önmaga lesz: `(x^2-4x)`

`(x^2-4x)+3=x^2+(-(x-5))`
Ez ugyanaz, mint a), tehát `x=-2/3` a megoldás. Viszont ez kívül esik az intervallumon, tehát ebben az intervallumban nincs megoldás.

c) 5 ≤ x:
• `x-5` pozitív: ezért |x-5|-ből önmaga lesz: `(x-5)`
• `x^2-4x` pozitív: (próbáld x=5-tel), önmaga lesz: `(x^2-4x)`
`(x^2-4x)+3=x^2+(x-5)`
`-4x+3=x-5`
`8=5x`
`x=5/8`

Ez nincs benne az intervallumban, nem megoldás.

Vagyis 3 megoldás volt:
`x_1=-2/3`
`x_2=1/2`
`x_3=2`

Meg kell nézni, ezeknél az x-eknél mennyi 6x+1 értéke, és azok közül mi a legkisebb:
`x_1=-2/3`  → `6x_1+1 = -4+1 = -3`
`x_2=1/2` → `6x_2+1 = 3+1 = 4`
`x_3=2` → `6x_3+1 = 12+1 = 13`

A legkisebb érték -3.