Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Egyenes
 sissypamacs
kérdése
sissypamacs
kérdése
515
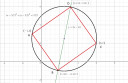
Egy négyzetben a szemközti csúcsok A(−1, 3) és C(6, 2). írjuk fel az oldalak egyenleteit.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 kazah
megoldása
kazah
megoldása
1. Illesszünk rá egy egyenest (szakaszt):
Az egyenes egyenlete:
3 = -m+b `rightarrow` b = 3+m
2 = 6m+b
1 = -5m
m = `-1/5`
2. A rá merőleges egyenes meredeksége: `m_2` = `-1/m` = `-1/(1/5)` = 5
3. A szakaszfelező pont koordinátái ami egyben a négyzet szimmetriaközéppontja):
`x_O` = `(x_A+x_C)/2` = `(-1+6)/2` = `5/2`
`y_O` = `(y_A+y_B)/2` = `(2+3)/2` = `5/2`
`O(5/2;5/2)`
4. A szakaszfelező merőleges egyenes egyenlete:
`5/2=5*5/2+b` `rightarrow` b = `(5-25)/2` = -10
y = `5x-10`
5. A négyzet csúcsai a szimmetriaközépponttól egyenlő távolságra vannak.
`d_(OA)` = `root()((x_O-x_A)^2+(y_O-y_A)^2)` = `root()((5/2+1)^2+(5/2-3)^2)` = `root()((7/2)^2+(1/2)^2)` = `root()(25/2)` = `5/2*root()(2)` = `d_(OB)` = `d_(OD)` = r
Az O középpontú kör és `d_(OA)` sugarú egyenes egyenlete:
`(x-5/2)^2+(y-5/2)^2=25/2`
y = 5x-10
A közös pontok lesznek a a négyzet két hiányzó csúcsa.
`(x-5/2)^2+(5x-10-5/2)^2=25/2`
`13x^2-80x+100=0`
Ezt szépen megoldod:
`x_B` = `(5*(13+root()(13)))/26` `approx` 3,19 `rightarrow` `y_B=5*4.41-10` `approx` 5,97
`x_D` = `(5*(13-root()(13)))/26` `approx` 1,81 `rightarrow` `y_D=5*1.81-10` `approx` -0,967
0
- Még nem érkezett komment!