Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek feladatsorban szeretnék segítséget
 chrabakkata90
kérdése
chrabakkata90
kérdése
346
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 kazah
megoldása
kazah
megoldása
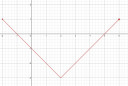
1,
Ábra
Értékkészlet: `y in [-3;1]`
Zérushely:
`|x-2|-3=0`
`|x-2|=3`
`x_1-2=3` `rightarrow` `x_1` = 5
`x_2-2=-3` `rightarrow` `x_2` = -1
Zérushelyek: (5;0) és (-1;0).
2,
`4^x=2^(x^2-3)`
`4^x=2^(2x)`
`2^(2x)=2^(x^2-3)`
Az alapok egyenlők, a kitevők is.
`2x=x^2-3`
`x^2-2x-3=0`
`(x-3)(x+1)=0`
Szorzat akkor nulla, ha valamelyik tényezője nulla.
`x_1` = 3
`x_2` = -1
Ellenőrizd!
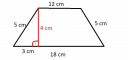
3,
Ábra
A berajzolt derékszögű háromszög oldalai kiszámolhatók:
`(18-12)/2` = 3 cm
A szög megállapításához ez is elég.
`cosalpha` = `3/5` = 0,6
`alpha` = 53,13°.
A másik szög: 180-`alpha` = 126,87°.
4,
`a_1` = 4
`a_5` = 48 = `a_1*q^4`
Elosztva a kettőt egymással:
`a_5/a_1` = `48/4` = 12 = `q^4`
`q_1` = `root(4)(12)`
`q_2` = `-root(4)(12)`
Ha q = `root(4)(12)`, akkor
`a_8` = `a_1*q^7` = kiszámolod, vagy egyszerűbb, ha `a_5`-től indulsz `a_8` = `a_5*q^3`;
Ugyanígy, ha `q=-root(4)(12)`, ugyanez lesz a megoldás, csak negatív előjellel.
5,
átlag: összeadod és osztod a darabszámmal. `bar(x)` = `(11+15+22+15+20+12+15+12+10)/9` = `14.dot(6)`.
módusz: leggyakrabban előforduló elem (15)
medián: sorbarakod a számokat és a középső elem.
10, 11, 12, 12, 15, 15, 15, 20, 22
9 elem van, az 5. elem a 15.
Ábra
Értékkészlet: `y in [-3;1]`
Zérushely:
`|x-2|-3=0`
`|x-2|=3`
`x_1-2=3` `rightarrow` `x_1` = 5
`x_2-2=-3` `rightarrow` `x_2` = -1
Zérushelyek: (5;0) és (-1;0).
2,
`4^x=2^(x^2-3)`
`4^x=2^(2x)`
`2^(2x)=2^(x^2-3)`
Az alapok egyenlők, a kitevők is.
`2x=x^2-3`
`x^2-2x-3=0`
`(x-3)(x+1)=0`
Szorzat akkor nulla, ha valamelyik tényezője nulla.
`x_1` = 3
`x_2` = -1
Ellenőrizd!
3,
Ábra
A berajzolt derékszögű háromszög oldalai kiszámolhatók:
`(18-12)/2` = 3 cm
A szög megállapításához ez is elég.
`cosalpha` = `3/5` = 0,6
`alpha` = 53,13°.
A másik szög: 180-`alpha` = 126,87°.
4,
`a_1` = 4
`a_5` = 48 = `a_1*q^4`
Elosztva a kettőt egymással:
`a_5/a_1` = `48/4` = 12 = `q^4`
`q_1` = `root(4)(12)`
`q_2` = `-root(4)(12)`
Ha q = `root(4)(12)`, akkor
`a_8` = `a_1*q^7` = kiszámolod, vagy egyszerűbb, ha `a_5`-től indulsz `a_8` = `a_5*q^3`;
Ugyanígy, ha `q=-root(4)(12)`, ugyanez lesz a megoldás, csak negatív előjellel.
5,
átlag: összeadod és osztod a darabszámmal. `bar(x)` = `(11+15+22+15+20+12+15+12+10)/9` = `14.dot(6)`.
módusz: leggyakrabban előforduló elem (15)
medián: sorbarakod a számokat és a középső elem.
10, 11, 12, 12, 15, 15, 15, 20, 22
9 elem van, az 5. elem a 15.
1
- Még nem érkezett komment!