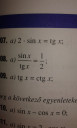Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Trigonometrikus egyenletek
 AnnaKv
kérdése
AnnaKv
kérdése
1037
Valaki tudna segiteni ezekben a masodfoku trigonometrikus egyenletekben? Levezetessel egyutt!!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 Velő Gábor
{ Matematikus }
válasza
Velő Gábor
{ Matematikus }
válasza
πππ1. 2*sinx=tgx / tgx=sinx/cosx
2*sinx=sinx/cosx / szorzunk cosx-szel, feltéve hogy cosx≠0-val
2*sinx*cosx=sinx /kivonunk mindkét oldalból sinx-et:
2*sinx*cosx-sinx=0 /kiemelünk sinx-et:
sinx*(2cox-1)=0 / egy szorzat akkor 0, ha valamelyik tényező 0, ezért
vagy: sinx=0 vagyis x=k*π
vagy: 2cosx-1=0 /+1
2cosx=1 /:2
cosx=0,5 /a koszinusz függvény 0⁰-360⁰ között két helyen veszi fel a 0,5-ös értéket: π/3-nál és 5π/3-nál. Így ennek az egyenletnek a megoldása:
x₁=π/3+k*2π és x₂=5π/3+l*2π, ahol k,l∈Z
Összesen tehát 3 megoldása volt ennek az egyenletnek!
2 sinx/tgx=1/2 /tgx≠0 (mert akkor értelmetlen lenne), ezért x≠k*π
szorzunk tgx-szel:
sinx=tgx/2 /szorzunk 2-vel:
2sinx=tgx /tgx=sinx/cosx
2sinx=sinx/cosx / szorzunk cosx-szel, feltéve hogy cosx≠0-val
2*sinx*cosx=sinx /kivonunk mindkét oldalból sinx-et:
2*sinx*cosx-sinx=0 /kiemelünk sinx-et:
sinx*(2cox-1)=0 / egy szorzat akkor 0, ha valamelyik tényező 0, ezért
vagy: sinx=0 vagyis x=k*π (azonban, ezt már kizártuk korábban)
vagy: 2cosx-1=0 /+1
2cosx=1 /:2
cosx=0,5 /a koszinusz függvény 0⁰-360⁰ között két helyen veszi fel a 0,5-ös értéket: π/3-nál és 5π/3-nál. Így ennek az egyenletnek a megoldása:
x₁=π/3+k*2π és x₂=5π/3+l*2π, ahol k,l∈Z
Ennek a feladatnak 2 megoldása volt.
3. tgx=ctgx / ctgx=1/tgx
tgx=1/tgx / tgx≠0, (mert akkor értelmetlen lenne), ezért x≠k*π
szorzunk tgx-szel:
tg²x=1, amiből tgx=1 vagy tgx=-1
ha tgx=1, akkor x=π/4+k*π
ha tgx=-1, akkor x=-π/4+k*π
Azonban a két megoldás pont egymás ellentétei, ezért elég felírni,hogy:
x=π/4+k*π/2=π/4*(1+2k)
2*sinx=sinx/cosx / szorzunk cosx-szel, feltéve hogy cosx≠0-val
2*sinx*cosx=sinx /kivonunk mindkét oldalból sinx-et:
2*sinx*cosx-sinx=0 /kiemelünk sinx-et:
sinx*(2cox-1)=0 / egy szorzat akkor 0, ha valamelyik tényező 0, ezért
vagy: sinx=0 vagyis x=k*π
vagy: 2cosx-1=0 /+1
2cosx=1 /:2
cosx=0,5 /a koszinusz függvény 0⁰-360⁰ között két helyen veszi fel a 0,5-ös értéket: π/3-nál és 5π/3-nál. Így ennek az egyenletnek a megoldása:
x₁=π/3+k*2π és x₂=5π/3+l*2π, ahol k,l∈Z
Összesen tehát 3 megoldása volt ennek az egyenletnek!
2 sinx/tgx=1/2 /tgx≠0 (mert akkor értelmetlen lenne), ezért x≠k*π
szorzunk tgx-szel:
sinx=tgx/2 /szorzunk 2-vel:
2sinx=tgx /tgx=sinx/cosx
2sinx=sinx/cosx / szorzunk cosx-szel, feltéve hogy cosx≠0-val
2*sinx*cosx=sinx /kivonunk mindkét oldalból sinx-et:
2*sinx*cosx-sinx=0 /kiemelünk sinx-et:
sinx*(2cox-1)=0 / egy szorzat akkor 0, ha valamelyik tényező 0, ezért
vagy: sinx=0 vagyis x=k*π (azonban, ezt már kizártuk korábban)
vagy: 2cosx-1=0 /+1
2cosx=1 /:2
cosx=0,5 /a koszinusz függvény 0⁰-360⁰ között két helyen veszi fel a 0,5-ös értéket: π/3-nál és 5π/3-nál. Így ennek az egyenletnek a megoldása:
x₁=π/3+k*2π és x₂=5π/3+l*2π, ahol k,l∈Z
Ennek a feladatnak 2 megoldása volt.
3. tgx=ctgx / ctgx=1/tgx
tgx=1/tgx / tgx≠0, (mert akkor értelmetlen lenne), ezért x≠k*π
szorzunk tgx-szel:
tg²x=1, amiből tgx=1 vagy tgx=-1
ha tgx=1, akkor x=π/4+k*π
ha tgx=-1, akkor x=-π/4+k*π
Azonban a két megoldás pont egymás ellentétei, ezért elég felírni,hogy:
x=π/4+k*π/2=π/4*(1+2k)
0
- Még nem érkezett komment!