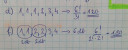Keresés


Toplista

Toplista
  • betöltés...

Magántanár kereső

Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!

Permutáció

Főoldal » Középiskola » Matematika
425
Sziasztok!

Ebben a feladatban szeretném a segítségeteket kérni:

Hányféle számot tudunk alkotni az alábbi számjegyek felhasználásával, ha az összes számjegyet fel kell használnunk?

a) 1, 1, 1, 2, 3, 4

b) 1, 1, 2, 2, 3, 4

A képen ott van, hogy hogyan oldottuk meg órán, de most valamiért mégsem tiszta.

Vegyük az a)-t:
a 6! = 6x5x4x3x2x1 = 720
a 3! = 3x2x1 =6
Azért osztom el a 720-at a 6-tal, mert 6-szor ugyanaz jönne ki a 6! permutációból a 3db 1-es miatt?

A b)-t is el tudnátok magyarázni?

Köszönöm szépen a segítséget előre is! <3
Permutáció – feladat kép 1
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika

Válaszok

1
1) Így van. A három 1-es ha más-más színű lenne, egymás között 3!-féle módon permutálódhatna, amik persze mind ugyanazt a 6 jegyű számot adják. Mivel a három 1-esen kívüli számok minden permutációjához hozzátartozik az 111 mind a 3! féle permutációja, osztani kell vele.

Nézzük egy kisebb számmal: 1₁, 1₂, 2
(Az alsó indexbe azért írtam számot, hogy meg lehessen különböztetni őket)
A permutációk:
1₁1₂2 → 112
1₂1₁2
1₁21₂ → 121
1₂21₁
21₁1₂ → 211
21₂1₁

A két 1-est 2! módon lehet egymással permutálni (sorbarakni), ezzel kellett a 3!=6-ot osztani.

b)
Itt most 1 és 2 is duplán van. Ha meg lennének ezek különböztetve, akkor 6! sorrend lenne. Abban viszont a két 1-esnek is 2! egymással vett sorrendje lehet, meg a két 2-esnek is, ezért 2!·2!-sal kell osztani.
1