Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Negyzetgyokos egyenletek
 AnnaKv
kérdése
AnnaKv
kérdése
1147
Ezt a ket egyenletet valaki megtudna nekem csinalni levezetessel, megoldassal, mindennel??
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 nono
válasza
nono
válasza
a) négyzetgyök(x^2 + 5x + 1) = 2x -1
1. Emeld négyzetre mindkét oldalt!
x^2 + 5x + 1 = (2x -1)^2
2. A jobb oldalt nevezetes azonossággal ki lehet fejteni.
x^2 + 5x + 1 = 4x^2 -4x +1
3. Rendezd egy oldalra a tagokat!
0 = 3x^2 - 9x
4. Ebből ki lehet emelni 3x-et.
0 = 3x*(x - 3)
5. Szorzat akkor nulla, ha valamelyik tényezője nulla. Tehát
- vagy 3x = 0 --> x=0
- vagy x-3 = 0 --> x = 3.
6. Ellenőrzés (fontos!).
- ha x=3 : négyzetgyök(25) = 5 = 6-1 --> ez oké.
- ha x=0 : négyzetgyök(1) = 1, viszont a jobb oldal 0-1=-1.
Tehát az x=0-val hamis gyököt kaptunk, mert a négyzetre emelés (1. lépés) nem ekvivalens átalakítás.
--------------------------------------------------------------------------------------------
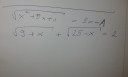
b) négyzetgyök(9+x) + négyzetgyök(25-x) = 2
1. Emeld négyzetre!
(négyzetgyök(9+x) + négyzetgyök(25-x))^2 = 2^2
2. A bal oldal nevezetes azonossággal kifejthető: (a+b)^2= a^2 + 2ab + b^2 . Itt most a= négyzetgyök(9+x), és b = négyzetgyök(25-x).
(9+x) + 2* négyzetgyök(9+x) * négyzetgyök(25-x) + (25-x) = 4
3. A négyzetgyökök szorzata összevonható.
9 + x + 2* négyzetgyök[(9+x)*(25-x)] + 25 - x = 4
4. Szerencsére a +x és -x tagok kiejtik egymást bal oldalon. A többit rendezd jobb oldalra, hogy bal oldalon már ne összeg, hanem csak egy négyzetgyök (többszöröse) maradjon!
2* négyzetgyök[(9+x)*(25-x)] = -30
5. Emeld négyzetre!
4* [(9+x)*(25-x)] = 900
6. Oszd el néggyel, majd fejtsd ki a zárójelben lévő szorzatot!
225 + 16 x - x^2 = 225
7. Rendezd 0-ra!
0 = x^2 -16x
8. Kiemelhető x:
0 = x * (x-16)
9. Szorzat akkor nulla, ha valamely tényezője nulla. Tehát:
- vagy x=0
- vagy x-16=0 --> x=16.
10. Ellenőrzés!
- ha x=16: négyzetgyök(25) + négyzetgyök(9) = 5 + 3 = 8 =/=2 , tehát ez hamis gyök.
- ha x=0: négyzetgyök(9) + négyzetgyök(25) = 3 + 5 = 8 =/=2, tehát ez is hamis gyök.
A bal oldalon szereplő függvénynek ezek szerint nem tud 2 lenni az értéke.
Erre a linkre kattintva láthatod a bal oldalon szereplő kifejezés ábrázolását: http://www.wolframalpha.com/input/?i=real+plot+(9%2Bx)%5E0.5+%2B+(25-x)%5E0.5+,+x%3D-80,+100 . (Sosem ér le 2-höz.)
1. Emeld négyzetre mindkét oldalt!
x^2 + 5x + 1 = (2x -1)^2
2. A jobb oldalt nevezetes azonossággal ki lehet fejteni.
x^2 + 5x + 1 = 4x^2 -4x +1
3. Rendezd egy oldalra a tagokat!
0 = 3x^2 - 9x
4. Ebből ki lehet emelni 3x-et.
0 = 3x*(x - 3)
5. Szorzat akkor nulla, ha valamelyik tényezője nulla. Tehát
- vagy 3x = 0 --> x=0
- vagy x-3 = 0 --> x = 3.
6. Ellenőrzés (fontos!).
- ha x=3 : négyzetgyök(25) = 5 = 6-1 --> ez oké.
- ha x=0 : négyzetgyök(1) = 1, viszont a jobb oldal 0-1=-1.
Tehát az x=0-val hamis gyököt kaptunk, mert a négyzetre emelés (1. lépés) nem ekvivalens átalakítás.
--------------------------------------------------------------------------------------------
b) négyzetgyök(9+x) + négyzetgyök(25-x) = 2
1. Emeld négyzetre!
(négyzetgyök(9+x) + négyzetgyök(25-x))^2 = 2^2
2. A bal oldal nevezetes azonossággal kifejthető: (a+b)^2= a^2 + 2ab + b^2 . Itt most a= négyzetgyök(9+x), és b = négyzetgyök(25-x).
(9+x) + 2* négyzetgyök(9+x) * négyzetgyök(25-x) + (25-x) = 4
3. A négyzetgyökök szorzata összevonható.
9 + x + 2* négyzetgyök[(9+x)*(25-x)] + 25 - x = 4
4. Szerencsére a +x és -x tagok kiejtik egymást bal oldalon. A többit rendezd jobb oldalra, hogy bal oldalon már ne összeg, hanem csak egy négyzetgyök (többszöröse) maradjon!
2* négyzetgyök[(9+x)*(25-x)] = -30
5. Emeld négyzetre!
4* [(9+x)*(25-x)] = 900
6. Oszd el néggyel, majd fejtsd ki a zárójelben lévő szorzatot!
225 + 16 x - x^2 = 225
7. Rendezd 0-ra!
0 = x^2 -16x
8. Kiemelhető x:
0 = x * (x-16)
9. Szorzat akkor nulla, ha valamely tényezője nulla. Tehát:
- vagy x=0
- vagy x-16=0 --> x=16.
10. Ellenőrzés!
- ha x=16: négyzetgyök(25) + négyzetgyök(9) = 5 + 3 = 8 =/=2 , tehát ez hamis gyök.
- ha x=0: négyzetgyök(9) + négyzetgyök(25) = 3 + 5 = 8 =/=2, tehát ez is hamis gyök.
A bal oldalon szereplő függvénynek ezek szerint nem tud 2 lenni az értéke.
Erre a linkre kattintva láthatod a bal oldalon szereplő kifejezés ábrázolását: http://www.wolframalpha.com/input/?i=real+plot+(9%2Bx)%5E0.5+%2B+(25-x)%5E0.5+,+x%3D-80,+100 . (Sosem ér le 2-höz.)
0
-
AnnaKv: Koszonom szepen.
 9 éve
0
9 éve
0