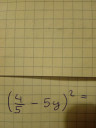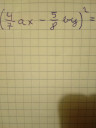Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Nevezetes szorzatok
 Ti
kérdése
Ti
kérdése
696
Ezt a kettőt levezetné valaki. Előre is köszi!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 bongolo
{
bongolo
{  }
válasza
}
válasza
http://www.wolframalpha.com/input/?i=(4%2F5+-+5y)%5E2
Az "Expanded form" alatt van a kifejtés.
A másikat is hasonlóan írd be.
Az "Expanded form" alatt van a kifejtés.
A másikat is hasonlóan írd be.
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
Ez egy (a-b)² alakú kifejezés. Ahhoz be kell ezt magolni:
(a-b)² = a² - 2ab + b²
Most ez van:
a=4/5
b = 5y
Ezeket kell a fentibe helyettesíteni. Darabonként:
A szorzatot és a hányadost egyesével lehet négyzetre emelni:
a² = (4/5)² = 16/25
b² = (5y)² = 25y²
Kell még a szorzatuk is:
2ab = 2·(4/5)·(5y) = 8y
Itt szoroztunk is 5-tel meg a nevezőben is vlt 5, azok kietették egymást.
Tehát az eredmény:
16/25 - 8y + 25y²
-----------------
A másik is ugyanilyen, csak mások az adatok:
a = 4/7 ax
b = 5/8 by
Huhh, ebben is van a meg b, de az nem ugyanaz az a meg b... Inkább másnak kellene neveznem, hogy ne legyen zavaró, kezdem előlről.
Ilyen alakú a kifejezés: (v-w)²
Ami kifejtve: v² - 2vw + w²
Ezt is be kell magolni!
Nem, nem igaz Természetesen mindegy, milyen betűket írunk bele, nem kell végtelen sokat bemagolni, csak az elvet.
Természetesen mindegy, milyen betűket írunk bele, nem kell végtelen sokat bemagolni, csak az elvet.
v² = (4/7 ax)² = 16/49 a²x²
w² = (5/8 by)² = 25/64 b²y²
2vw = 2·(4/7 ax)·(5/8 by) = ... magyarázom:
Ez a 4/7 meg 5/8 nem látszik itt elég jól, a papírodon ha leírod, sokkal érthetőbb lesz. A 4 a számlálóban van, a 8 a nevezőben, lehet 4-gyel egyszerűsíteni:
2vw = 2 · 1/7 ax · 5/2 by = ...
Aztán szorozva van 2-vel, és a nevezőben is van még 2, azokkal is lehet egyszerűsíteni:
= 1/7 ax · 5/1 by
Több egyszerűsítés nem lehet. Szorozzuk össze a számlálókat meg amik törtön kívül vannak, ez lesz a végső számláló, aztán szorozzuk össze a nevezőket, az lesz a végső nevező:
= 5axby / 7
A teljes négyzet pedig:
16/49 a²x² - 5axby/7 + 25/64 b²y²
(a-b)² = a² - 2ab + b²
Most ez van:
a=4/5
b = 5y
Ezeket kell a fentibe helyettesíteni. Darabonként:
A szorzatot és a hányadost egyesével lehet négyzetre emelni:
a² = (4/5)² = 16/25
b² = (5y)² = 25y²
Kell még a szorzatuk is:
2ab = 2·(4/5)·(5y) = 8y
Itt szoroztunk is 5-tel meg a nevezőben is vlt 5, azok kietették egymást.
Tehát az eredmény:
16/25 - 8y + 25y²
-----------------
A másik is ugyanilyen, csak mások az adatok:
a = 4/7 ax
b = 5/8 by
Huhh, ebben is van a meg b, de az nem ugyanaz az a meg b... Inkább másnak kellene neveznem, hogy ne legyen zavaró, kezdem előlről.
Ilyen alakú a kifejezés: (v-w)²
Ami kifejtve: v² - 2vw + w²
Ezt is be kell magolni!
Nem, nem igaz
 Természetesen mindegy, milyen betűket írunk bele, nem kell végtelen sokat bemagolni, csak az elvet.
Természetesen mindegy, milyen betűket írunk bele, nem kell végtelen sokat bemagolni, csak az elvet.v² = (4/7 ax)² = 16/49 a²x²
w² = (5/8 by)² = 25/64 b²y²
2vw = 2·(4/7 ax)·(5/8 by) = ... magyarázom:
Ez a 4/7 meg 5/8 nem látszik itt elég jól, a papírodon ha leírod, sokkal érthetőbb lesz. A 4 a számlálóban van, a 8 a nevezőben, lehet 4-gyel egyszerűsíteni:
2vw = 2 · 1/7 ax · 5/2 by = ...
Aztán szorozva van 2-vel, és a nevezőben is van még 2, azokkal is lehet egyszerűsíteni:
= 1/7 ax · 5/1 by
Több egyszerűsítés nem lehet. Szorozzuk össze a számlálókat meg amik törtön kívül vannak, ez lesz a végső számláló, aztán szorozzuk össze a nevezőket, az lesz a végső nevező:
= 5axby / 7
A teljes négyzet pedig:
16/49 a²x² - 5axby/7 + 25/64 b²y²
Módosítva: 8 éve
0
-
Ti: Huuuuuu hát ezt nem értem, bekeveredtem a vw- nél 8 éve 0
-
bongolo: Akkor felejtsd el a vw-t, maradj az ab-nél, hátha nem zavar... 8 éve 0