Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Kérlek
 richard-nagy4130
kérdése
richard-nagy4130
kérdése
495
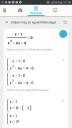
Valós számok halmazán
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 Rantnad
{
Rantnad
{  }
válasza
}
válasza
Először azt a kérdést kellene megválaszolni, hogy egy törtértéke mikor 0; akkor, ha a számlálója 0, tehát -x+1=0, ennek a megoldása x=1.
Ellenőrzés: (-1+1)/(1²+4*1+4)=0/9=0, ez jó megoldás.
Most az a kérdés, hogy mikor nagyobb, mint 0; akkor ha pozitív. És mikor pozitív? Akkor, hogyha a számláló és a nevező előjele azonos, tehát vagy mindkettő pozitív, vagy mindkettő negatív. Ennek fényében két esetre bomlik a feladat:
1. eset: mindkettő pozitív, tehát -x+1>0 és x²+4x+4>0. az első egyenlőtlenséget meg tudjuk oldani: 1>x, a másodiknál azt érdemes észrevenni, hogy egy teljes négyzet, (x+2)² van, tehát (x+2)²>0. Mivel a 0 kivételével minden szám négyzete poztiív, ezért a 0-t kivéve minden szám jó lesz, 0²=0, ami nem nagyobb 0-nál, tehát ha x+2 értéke 0, vagyis ha x értéke -2, akkor nem lesz megoldás. Összevetve a két megoldáshalmazt, azt kapjuk hogy a -2-t kivéve a -1-nél kisebb számok igazzá teszik az egyenlőtlenséget.
2. eset: mindkettő negatív, tehát -x+1<0 és x²+4x+4<0, viszont az előbb leírtuk, hogy az utóbbi minden x-re leaglább 0, tehát ebben az esetben nem fogunk megoldást találni.
Összevetve a különböző esetekben talált megoldásokat, azt kapjuk, hogy x≤-1, de x≠-2 esetén valósul meg az egyenlőtlenség.
Ellenőrzés: (-1+1)/(1²+4*1+4)=0/9=0, ez jó megoldás.
Most az a kérdés, hogy mikor nagyobb, mint 0; akkor ha pozitív. És mikor pozitív? Akkor, hogyha a számláló és a nevező előjele azonos, tehát vagy mindkettő pozitív, vagy mindkettő negatív. Ennek fényében két esetre bomlik a feladat:
1. eset: mindkettő pozitív, tehát -x+1>0 és x²+4x+4>0. az első egyenlőtlenséget meg tudjuk oldani: 1>x, a másodiknál azt érdemes észrevenni, hogy egy teljes négyzet, (x+2)² van, tehát (x+2)²>0. Mivel a 0 kivételével minden szám négyzete poztiív, ezért a 0-t kivéve minden szám jó lesz, 0²=0, ami nem nagyobb 0-nál, tehát ha x+2 értéke 0, vagyis ha x értéke -2, akkor nem lesz megoldás. Összevetve a két megoldáshalmazt, azt kapjuk hogy a -2-t kivéve a -1-nél kisebb számok igazzá teszik az egyenlőtlenséget.
2. eset: mindkettő negatív, tehát -x+1<0 és x²+4x+4<0, viszont az előbb leírtuk, hogy az utóbbi minden x-re leaglább 0, tehát ebben az esetben nem fogunk megoldást találni.
Összevetve a különböző esetekben talált megoldásokat, azt kapjuk, hogy x≤-1, de x≠-2 esetén valósul meg az egyenlőtlenség.
1
- Még nem érkezett komment!