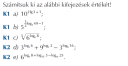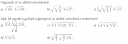Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Logaritmus
 Hermész
kérdése
Hermész
kérdése
549
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 gyula205
megoldása
gyula205
megoldása
Az első feladatcsoport mindegyike a logaritmus egyik elnyelési tulajdonságához
köthető. Ezekből az egyik: `a,b >0` és `a ne 1` esetén `a^(log_a b)=b`.
Míg a másik: `a,b >0` és `a ne 1` esetén `log_a a^b=b`.
Persze tudni kell használni a hatványokra és a logaritmikus
kifejezésekre vonatkozó azonosságokat is.
a.) `10^(2*lg 3+1)=10^(lg 9+1)=10*10^(lg 9)=10*9=90`;
b.) `5^(frac{1}{2}*log_5 49-1)=5^(log_5 sqrt(49)-1)=frac{7}{5}`;
c.) `root(3) (6^(log_6 8))=root(3) 8=2`;
d.) `3^(log_3 6)+9^(log_3 2)-3^(log_9 16)=6+3^(2*(log_3 2))-3^(2*log_9 4)=`
`=6+3^(log_3 4)-9^(log_9 4)=6+4-4=6`;
e.) `6^(log_6 8+log_sqrt(6) 3+log_(36) 25)=6^(log_6 8)*6^(2*log_6 3)*6^(frac{1}{2}*log_6 25)=`
`=8*9*5=360`.
A másik feladatcsoport nem kapcsolható a logaritmus azonosságaihoz, csak
a gyökökre és hatványokra vonatkozó azonosságokat kell tudni alkalmazni.
1/a.) `sqrt(root(3) 6)*root(4) sqrt(10)=6^(frac{1}{3}*frac{1}{2})*10^(frac{1}{2}*frac{1}{4})=`
`=2^frac{1}{6}*3^frac{1}{6}*2^frac{1}{8}*5^frac{1}{8}=2^frac{4+3}{24}*3^frac{1}{6}*5^frac{1}{8}=root(24)(2^7)*root(6) 3*root(8) 5`;
1/b.) `sqrt(root(4) frac{1}{2})*root(5) sqrt(2^3)=2^(-frac{1}{4*2})*2^(frac{3}{2*5})=2^(frac{3}{10}-frac{1}{8})=2^frac{12-5}{40}=root(40) (2^7)`;
1/c.) `sqrt(root(5) frac{1}{3})^5*root(4) sqrt(3^3)=3^(-frac{5}{5*2})*3^(frac{3}{2*4})=3^(frac{3}{8}-frac{1}{2})=3^frac{3-4}{8}=root(8) (3^(-1))=frac{1}{3}root(8)(3^7)`;
2/a.) `frac{root(4)2*root(5)2*root(3)4}{sqrt(frac{1}{8})}=2^(frac{1}{4}+frac{1}{5}+frac{2}{3}-frac{-3}{2})=2^(frac{15+12+20+30}{60}=root(60)(2^77)`;
2/b.) `root(4)(3sqrt(3))=root(4)3*root(8)3=3^(frac{1}{4}+frac{1}{8})=3^frac{3}{8}=root(8)27`;
2/c.) `root(3)(5*root(5)(125*root(4)5))=root(3)5*root(5*3)(5^3)*root(60)(5)=5^(frac{1}{3}+frac{1}{5}+frac{1}{60})=5^frac{20+12+1}{60}=root(60)(5^33)`;
2/d.) `root(3)(frac{2}{3}*sqrt(frac{3}{2}*root(3)6))=(frac{3}{2})^(frac{1}{6}-frac{1}{3})*6^frac{1}{18}=`
`=(frac{3}{2})^(-frac{1}{6})*6^frac{1}{18}=(frac{3}{2})^(-frac{3}{18})*6^frac{1}{18}=root(18)((frac{2}{3})^3*2*3)=root(18)(frac{2^4}{3^2})=root(9)(frac{4}{3})`;
2/e.) `sqrt(a^3*sqrt(a*root(4)(a^2)))=a^(frac{3}{2}+frac{1}{4}+frac{1}{8})=a^frac{12+2+1}{8}=root(8)(a^15)` és `a>0`.
köthető. Ezekből az egyik: `a,b >0` és `a ne 1` esetén `a^(log_a b)=b`.
Míg a másik: `a,b >0` és `a ne 1` esetén `log_a a^b=b`.
Persze tudni kell használni a hatványokra és a logaritmikus
kifejezésekre vonatkozó azonosságokat is.
a.) `10^(2*lg 3+1)=10^(lg 9+1)=10*10^(lg 9)=10*9=90`;
b.) `5^(frac{1}{2}*log_5 49-1)=5^(log_5 sqrt(49)-1)=frac{7}{5}`;
c.) `root(3) (6^(log_6 8))=root(3) 8=2`;
d.) `3^(log_3 6)+9^(log_3 2)-3^(log_9 16)=6+3^(2*(log_3 2))-3^(2*log_9 4)=`
`=6+3^(log_3 4)-9^(log_9 4)=6+4-4=6`;
e.) `6^(log_6 8+log_sqrt(6) 3+log_(36) 25)=6^(log_6 8)*6^(2*log_6 3)*6^(frac{1}{2}*log_6 25)=`
`=8*9*5=360`.
A másik feladatcsoport nem kapcsolható a logaritmus azonosságaihoz, csak
a gyökökre és hatványokra vonatkozó azonosságokat kell tudni alkalmazni.
1/a.) `sqrt(root(3) 6)*root(4) sqrt(10)=6^(frac{1}{3}*frac{1}{2})*10^(frac{1}{2}*frac{1}{4})=`
`=2^frac{1}{6}*3^frac{1}{6}*2^frac{1}{8}*5^frac{1}{8}=2^frac{4+3}{24}*3^frac{1}{6}*5^frac{1}{8}=root(24)(2^7)*root(6) 3*root(8) 5`;
1/b.) `sqrt(root(4) frac{1}{2})*root(5) sqrt(2^3)=2^(-frac{1}{4*2})*2^(frac{3}{2*5})=2^(frac{3}{10}-frac{1}{8})=2^frac{12-5}{40}=root(40) (2^7)`;
1/c.) `sqrt(root(5) frac{1}{3})^5*root(4) sqrt(3^3)=3^(-frac{5}{5*2})*3^(frac{3}{2*4})=3^(frac{3}{8}-frac{1}{2})=3^frac{3-4}{8}=root(8) (3^(-1))=frac{1}{3}root(8)(3^7)`;
2/a.) `frac{root(4)2*root(5)2*root(3)4}{sqrt(frac{1}{8})}=2^(frac{1}{4}+frac{1}{5}+frac{2}{3}-frac{-3}{2})=2^(frac{15+12+20+30}{60}=root(60)(2^77)`;
2/b.) `root(4)(3sqrt(3))=root(4)3*root(8)3=3^(frac{1}{4}+frac{1}{8})=3^frac{3}{8}=root(8)27`;
2/c.) `root(3)(5*root(5)(125*root(4)5))=root(3)5*root(5*3)(5^3)*root(60)(5)=5^(frac{1}{3}+frac{1}{5}+frac{1}{60})=5^frac{20+12+1}{60}=root(60)(5^33)`;
2/d.) `root(3)(frac{2}{3}*sqrt(frac{3}{2}*root(3)6))=(frac{3}{2})^(frac{1}{6}-frac{1}{3})*6^frac{1}{18}=`
`=(frac{3}{2})^(-frac{1}{6})*6^frac{1}{18}=(frac{3}{2})^(-frac{3}{18})*6^frac{1}{18}=root(18)((frac{2}{3})^3*2*3)=root(18)(frac{2^4}{3^2})=root(9)(frac{4}{3})`;
2/e.) `sqrt(a^3*sqrt(a*root(4)(a^2)))=a^(frac{3}{2}+frac{1}{4}+frac{1}{8})=a^frac{12+2+1}{8}=root(8)(a^15)` és `a>0`.
Módosítva: 4 éve
0
-
Hermész: Köszi haver 4 éve 0