A faktoriális egy lehetséges definiálása a következő alakot eredményezi:
`beta_(n+1)=sum_(k=0)^n ((n),(k))*beta_k*beta_(n-k)` és `beta_0=1`.
Itt `beta_n=n!`.

A felsőbb matematikában használatos még a pszeudo-faktoriális is, amelynek definiálása következő alakú:
`alpha_(n+1)=(-1)^(n+1)*sum_(k=0)^n ((n),(k))*alpha_k*alpha_(n-k)` és `alpha_0=1`.
Ebből az első néhány elem így néz ki: `1, -1, -2, 2, 16, -40, -320, 1040, 12160, ...` (OEIS A098777)

Keressünk a fenti implicit definícón kivül valamilyen
másfajta explicit vagy rekurzív kifejezést a pszeudofaktoriális megadására!

Leírnám, hogy kutakodásaim során meddig jutottam el. Ebből a kétféle faktoriálisból előállítottam egy kétváltozós polinomsorozatot a következőféleképpen:

`delta_n=((-1)^n*y+x)*sum_(k=0)^(n-1)((n-1),(k))*delta_k*delta_(n-1-k)` és `delta_0=1`.

Ennek első hat eleme szorzat alakban:
`1, x - y, 2·(y + x)·(x - y), 2·(y - x)^2·(y + 3·x),`
`8·(y + x)·(y - x)^2·(2·y + 3·x),`
`8·(x - y)^3·(5·y^2 + 12·y·x +15·x^2),...` stb.

Ugyanez zárójelek nélkül:
`1, - y+x,`
`-2·y^2 + 2·x^2, 2·y^3 + 2·y^2·x - 10·y·x^2 + 6·x^3,`
`16·y^4 + 8·y^3·x - 40·y^2·x^2 - 8·y·x^3 + 24·x^4,`
`- 40·y^5 + 24·y^4·x + 48·y^3·x^2 + 112·y^2·x^3 - 264·y·x^4 + 120·x^5,` `...` stb.

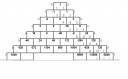
A polinomok együtthatóit a Pascal háromszöghöz hasonló elrendezésbe hoztam, amely a csatolt képen olvasható. A 0-ás sor kivételével háromszög együtthatóit soronként összeadva (legalább is az első 14 sornál) zérust eredményezett. Sejtésem az, hogy tetszőleges sor esetén is igaz az együtthatók összege zérust ad. Ennek bizonyítása talán közelebb vinne a megoldáshoz vezető úton. Azt kellene bizonyítani, hogy `forall n`-re `delta(n) equiv 0 mod(x-y)`. Továbbá észrevehető, hogy a háromszög jobb szélén a hagyományos, míg a bal szélén a pszeudo változatok találhatók. A sorok utolsó két elemére észrevehető egy rekurzió, amelyet a felette lévő két elemből származtathatunk. A legtriviálisabb a hagyományos faktoriálishoz tartozó rekurzió: `(n+1)!` `=(n+1)*n!`. Együtthatókhoz tartozó szorzótényezők jobbról bal irányba haladva a következő három csoportba sorolhatók: `n+1, (-1)^(n+1)*(2n+1)` és `n+2`. Minden háromszögön belüli együtthatóhoz két szorzótényező is tartozik. Például a 4!=24 melletti -8-as együtthatót a felette lévő -10-es és 6-os együtthatóból származtatható úgy, hogy megszorozzuk őket 5-el és 7-el, majd összevonjuk őket. Tehát `5*(-10)+7*6=-8`. Hasonló tulajdonságot várhatunk a többi elem esetén is. A probléma nehézségére való tekintettel örömmel veszek minden olyan ötletet, amelyek segítségével megoldható ez a feladat, amit előre is megköszönnék.