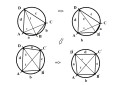
Bizonyítsuk be, hogy egy tetszőleges sugarú körön ugyanazokkal az `(a, b, c, d)` oldalakkal lényegében háromféle húrnégyszög
konstruálható. Elkészítettem egyfajta bizonyítást (lásd a csatolt ábrát) az `a` oldal jobboldali szomszédos oldalának a cseréjével. Lényegében három esetet kaptam: `(a, b, c, d)=>(b, a, c, d)=>(b, c, a, d)=>(a, b, c, d)`. Ugyanez elvégezhető a húrnégyszög tengelyre tükrözött az eredetivel egybevágó húrnégyszögével is. Nem nehéz belátni, hogy az így kapott hat darab húrnégyszög három darabra (páronként tengelyes tükrözéssel) egyszerűsíthető. A kapott transzformációk során lássuk
be, hogy a három darab húrnégyszög négy oldala `(a, b, c, d)` a háromféle átlóval `(e, f, g)` a Ptolemaiosz-tétel alkalmazásával a
következő összefüggést adja:

`(a+b+c+d)^2-(e+f+g)^2=(a^2+b^2+c^2+d^2)-(e^2+f^2+g^2)`

Végezetül bizonyítsuk be a három húrnégyszögre felállítható Pitagorasz-tételt abban az esetben, ha az (a, b, c, d) oldalak közül a `d` a kör átmérője: `a^2+b^2+c^2+e^2+f^2+g^2=3d^2`.

Hasonló sejtést kaptam a húrötszögek esetére. Itt a transzformácókkal a d átmérőn kivül négy oldallal és 10 átlóval számoltam:
`sum_(i=1)^4 a_i^2+sum_(i=1)^10 e_i^2=7d^2`
Ha valaki ezt be tudná bizonyítani, nagyon megköszönném.